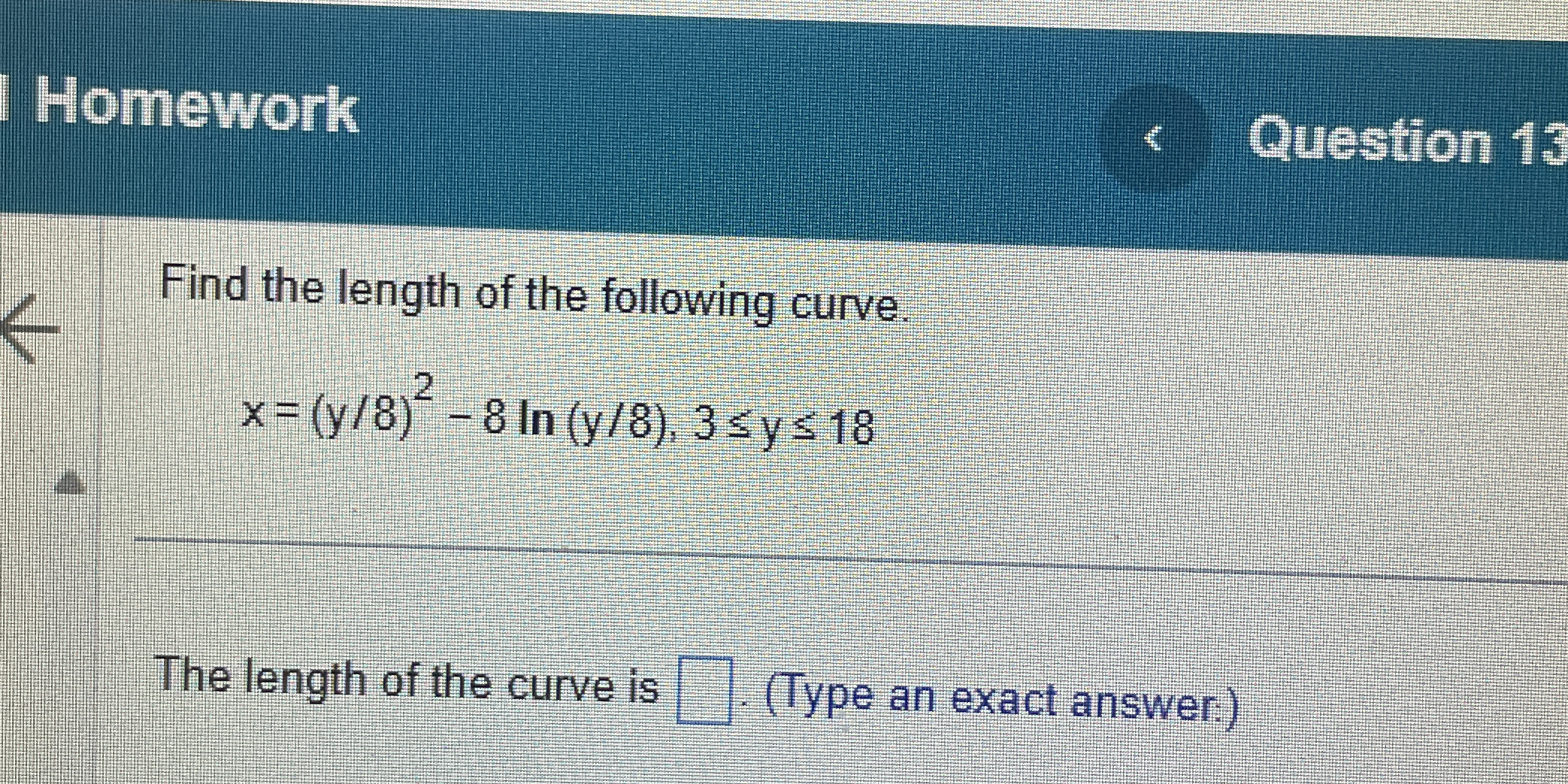
Find the length of the following curve: x = (y/8)² - 8 ln(y/8), 3 ≤ y ≤ 18.

Steps to Solve

1. Set Up the Arc Length Formula

To find the length of the curve defined by $x = \left( \frac{y}{8} \right)^{2} - 8 \ln\left( \frac{y}{8} \right)$ over the interval $3 \leq y \leq 18$, we use the arc length formula for a curve given in the form $x(y)$:

$$ L = \int_{a}^{b} \sqrt{1 + \left( \frac{dx}{dy} \right)^{2}} , dy $$

Here, $a = 3$ and $b = 18$.

2. Calculate the Derivative $\frac{dx}{dy}$

We need to differentiate $x$ with respect to $y$:

$$ x = \left( \frac{y}{8} \right)^{2} - 8 \ln\left( \frac{y}{8} \right) $$

Using the derivative rules:

$$ \frac{dx}{dy} = \frac{1}{8}(y) - 8 \cdot \frac{1}{y} \cdot \frac{1}{8} $$

Simplifying this gives:

$$ \frac{dx}{dy} = \frac{y}{8} - 1 $$

3. Substitute $\frac{dx}{dy}$ into the Arc Length Formula

Now substitute $\frac{dx}{dy}$ into the arc length formula:

$$ L = \int_{3}^{18} \sqrt{1 + \left(\frac{y}{8} - 1 \right)^{2}} , dy $$

4. Simplify the Expression Inside the Integral

Simplify the expression inside the square root:

$$ \left(\frac{y}{8} - 1 \right)^{2} = \left(\frac{y - 8}{8}\right)^{2} = \frac{(y - 8)^{2}}{64} $$

So:

$$ L = \int_{3}^{18} \sqrt{1 + \frac{(y - 8)^{2}}{64}} , dy $$

5. Evaluate the Integral

This integral can be solved using numerical methods or further calculus techniques, resulting in a specific length value.