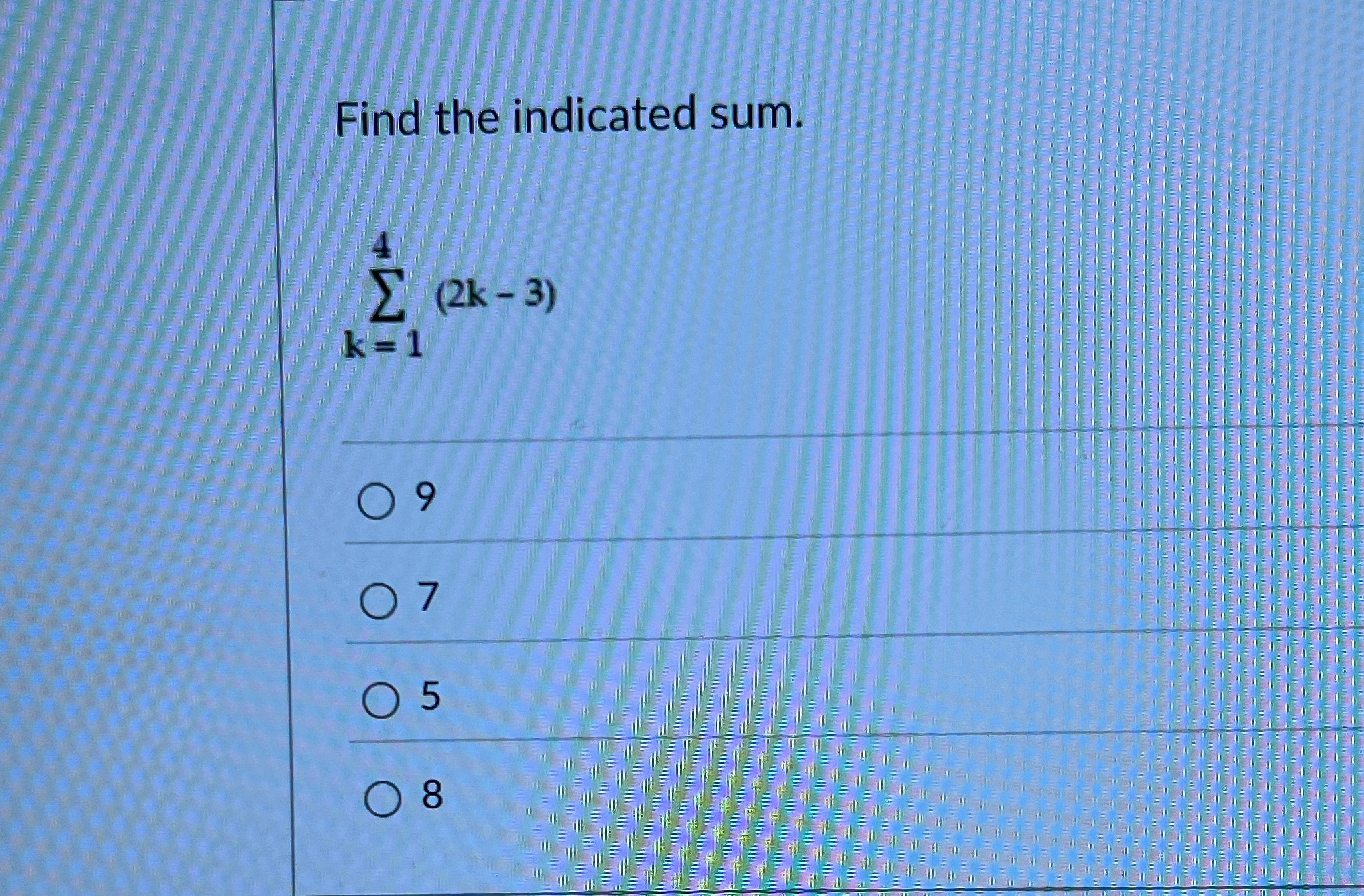
Find the indicated sum. Σ (2k - 3) from k=1 to 4.
Understand the Problem
The question is asking to find the sum of the expression (2k - 3) as k runs from 1 to 4. This involves calculating the individual values of the expression for each k and then adding them together.
Answer
The sum is \(8\).
Answer for screen readers
The indicated sum is (8).
Steps to Solve
-
Identify the expression and range We need to evaluate the expression (2k - 3) for (k) from 1 to 4.
-
Calculate individual terms We will compute (2k - 3) for each integer value of (k) in the specified range.
- For (k = 1): $$ 2(1) - 3 = 2 - 3 = -1 $$
- For (k = 2): $$ 2(2) - 3 = 4 - 3 = 1 $$
- For (k = 3): $$ 2(3) - 3 = 6 - 3 = 3 $$
- For (k = 4): $$ 2(4) - 3 = 8 - 3 = 5 $$
-
Sum the results Now, add all the computed terms together: $$ -1 + 1 + 3 + 5 $$ Calculating this gives: $$ -1 + 1 = 0 $$ Then: $$ 0 + 3 = 3 $$ And finally: $$ 3 + 5 = 8 $$
The indicated sum is (8).
More Information
The expression ( \sum_{k=1}^{4} (2k - 3) ) calculates the sum of values obtained by substituting ( k ) from 1 to 4 into ( 2k - 3 ). It’s a common exercise in summation notation to evaluate such series.
Tips
- Not substituting the correct values for (k) can lead to incorrect sums.
- Forgetting to perform the calculations step-by-step may result in miscalculation of the final sum.
AI-generated content may contain errors. Please verify critical information