Find the height of the tree. Show your work algebraically.
Understand the Problem
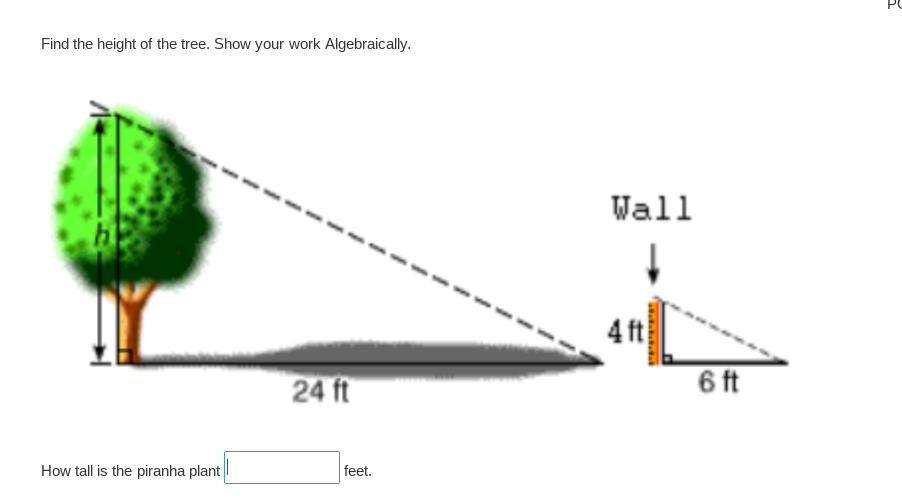
The question is asking to find the height of a tree using algebraic methods based on the information given in the image. To solve it, we will apply trigonometric principles, likely using right triangle relationships.
Answer
The tree is $16 \text{ ft}$ tall.
Answer for screen readers
The height of the tree, $h$, is ( 16 \text{ ft} ).
Steps to Solve
-
Understanding the Geometry
We have two triangles involved: the triangle formed by the tree and the ground, and the triangle formed by the wall and the ground. -
Setting Up the Right Triangle for the Tree
The height of the tree is represented as $h$, and the distance from the foot of the tree to the point on the ground where the top of the tree’s shadow lies is 24 ft. -
Setting Up the Right Triangle for the Wall
In the right triangle formed by the wall, the height of the wall is 4 ft and its distance from the base to the point directly below the top of the wall is 6 ft. -
Using the Tangent Function
For the wall triangle, the tangent of the angle $\theta$ can be expressed as: $$ \tan(\theta) = \frac{4 \text{ ft}}{6 \text{ ft}} $$ -
Calculating the Tangent Ratio
We calculate the tangent: $$ \tan(\theta) = \frac{2}{3} $$ -
Finding the Height of the Tree
Using the tangent principle for the tree: $$ \tan(\theta) = \frac{h}{24 \text{ ft}} $$ Thus, $$ h = 24 \text{ ft} \cdot \tan(\theta) $$ -
Substituting the Tangent Value
Now substitute $\tan(\theta) = \frac{2}{3}$: $$ h = 24 \text{ ft} \cdot \frac{2}{3} $$ -
Calculating $h$
Calculating the height: $$ h = 24 \cdot \frac{2}{3} = 16 \text{ ft} $$
The height of the tree, $h$, is ( 16 \text{ ft} ).
More Information
The problem illustrates the application of trigonometric functions to real-world scenarios, showing how right triangles can be used to derive heights that are otherwise difficult to measure directly.
Tips
- Confusing the ratios of the triangle; always ensure to match the correct opposite and adjacent sides when using tangent functions.
- Forgetting to solve for the variable $h$ properly. It’s crucial to rearrange equations correctly.
AI-generated content may contain errors. Please verify critical information