Find the equation of the equation with the root (α² - β²) = 3 and α - β = 2.
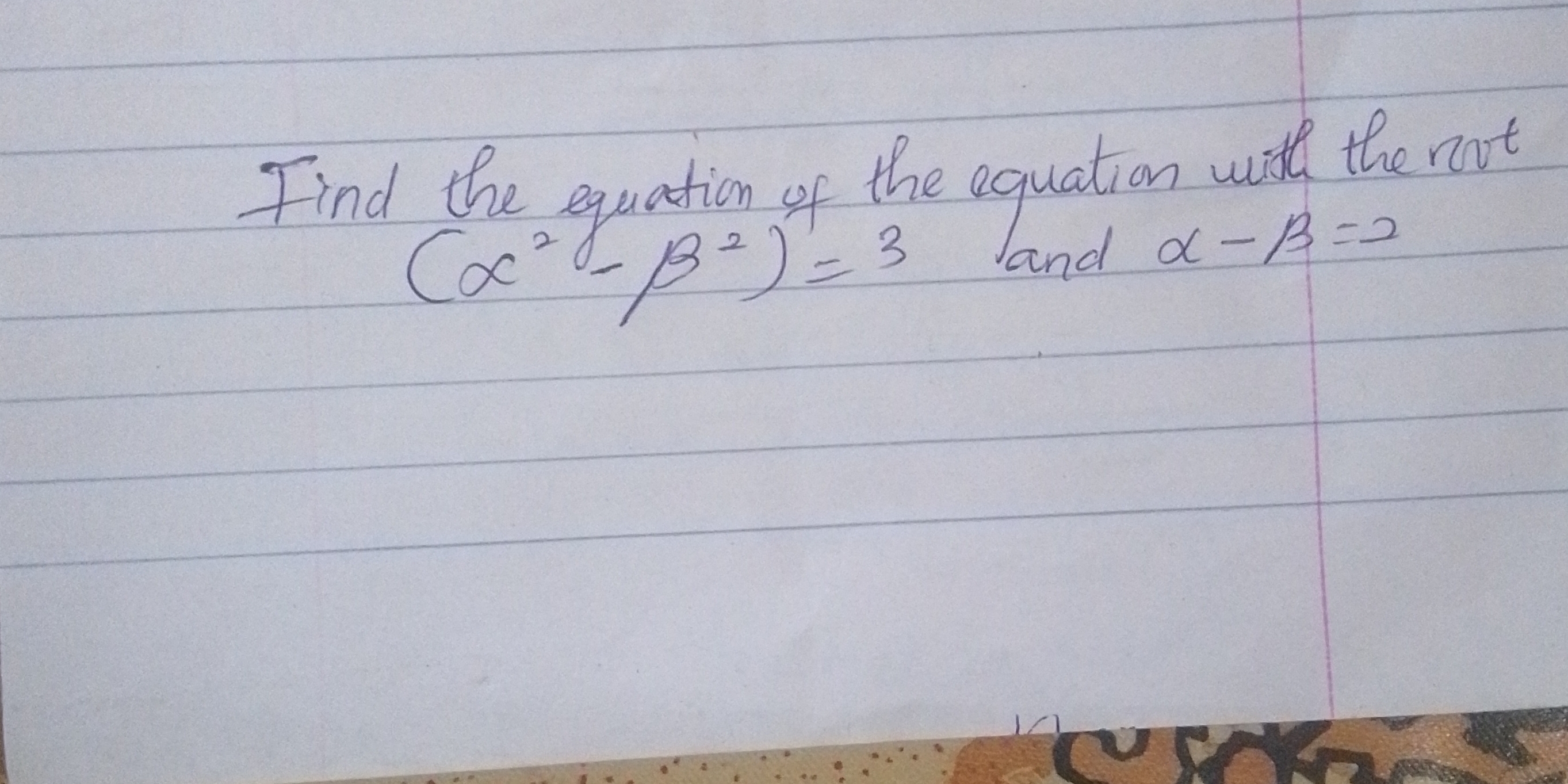
Understand the Problem
The question is asking to find the equation related to the given roots involving the expressions α² - β² = 3 and α - β = 2. This involves algebraic manipulation and understanding of the relationships between roots.
Answer
The quadratic equation is \( 16x^2 - 24x - 7 = 0 \).
Answer for screen readers
The equation of the quadratic is given by:
$$ 16x^2 - 24x - 7 = 0 $$
Steps to Solve
-
Use the given equations We have two equations:
- ( \alpha^2 - \beta^2 = 3 )
- ( \alpha - \beta = 2 )
-
Express ( \alpha ) using ( \beta ) From the equation ( \alpha - \beta = 2 ), we can express ( \alpha ): $$ \alpha = \beta + 2 $$
-
Substitute ( \alpha ) in the first equation Now substitute ( \alpha ) in the equation ( \alpha^2 - \beta^2 = 3 ): $$ (\beta + 2)^2 - \beta^2 = 3 $$
-
Expand the equation Expanding the left side gives: $$ \beta^2 + 4\beta + 4 - \beta^2 = 3 $$
-
Simplify the equation This simplifies to: $$ 4\beta + 4 = 3 $$
-
Solve for ( \beta ) Isolate ( \beta ): $$ 4\beta = 3 - 4 $$ $$ 4\beta = -1 $$ $$ \beta = -\frac{1}{4} $$
-
Find ( \alpha ) Now substitute ( \beta ) back to find ( \alpha ): $$ \alpha = -\frac{1}{4} + 2 = \frac{7}{4} $$
-
Form the equation The sum of roots ( s = \alpha + \beta ) and product of roots ( p = \alpha \beta ) can now be calculated: $$ s = \frac{7}{4} - \frac{1}{4} = \frac{6}{4} = \frac{3}{2} $$ $$ p = \frac{7}{4} \cdot \left(-\frac{1}{4}\right) = -\frac{7}{16} $$
-
Write the quadratic equation The quadratic equation can be formed as: $$ x^2 - sx + p = 0 $$ Substituting for ( s ) and ( p ): $$ x^2 - \frac{3}{2}x - \frac{7}{16} = 0 $$
-
Clear the fractions by multiplying by 16 Multiplying the equation throughout by 16 to eliminate fractions: $$ 16x^2 - 24x - 7 = 0 $$
The equation of the quadratic is given by:
$$ 16x^2 - 24x - 7 = 0 $$
More Information
This quadratic equation is derived from the relationships between the roots ( \alpha ) and ( \beta ). The solution demonstrates the connection between the values of the roots and their sum and product, a fundamental concept in algebra.
Tips
null
AI-generated content may contain errors. Please verify critical information