Find the directional derivative of V^2 = V ⋅ V, where V = xy^2 i + zy^2 j + xz^2 k at the point (2,0,3) in the direction of the outward normal to the sphere x^2 + y^2 + z^2 = 14 at... Find the directional derivative of V^2 = V ⋅ V, where V = xy^2 i + zy^2 j + xz^2 k at the point (2,0,3) in the direction of the outward normal to the sphere x^2 + y^2 + z^2 = 14 at the point (3,2,1).
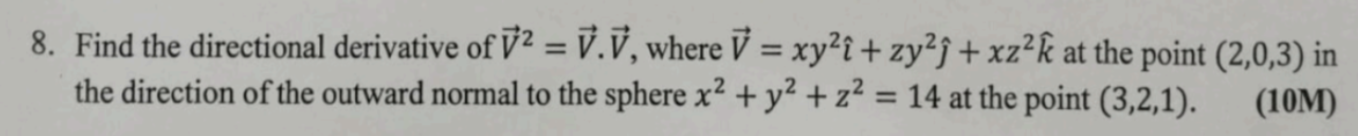
Understand the Problem
The question is asking to find the directional derivative of a vector field at a specific point, taking into account the normal direction to a sphere defined by an equation. This involves applying principles of vector calculus.
Answer
The directional derivative is \( \frac{66}{7} \sqrt{14} \).
Answer for screen readers
The directional derivative is:
$$ \frac{66}{7} \sqrt{14} $$
Steps to Solve
- Calculate the Gradient of the Vector Field
First, we need to compute the gradient of the scalar function represented by the vector field ( V ). Here, we have:
$$ V = xy^2 , \hat{i} + zy^2 , \hat{j} + xz^2 , \hat{k} $$
To find the directional derivative, we first find ( \nabla V^2 ).
Using the product rule:
$$ V^2 = V \cdot V = (xy^2)^2 + (zy^2)^2 + (xz^2)^2 $$
We can calculate the gradient:
$$ \nabla V^2 = \left( \frac{\partial V^2}{\partial x}, \frac{\partial V^2}{\partial y}, \frac{\partial V^2}{\partial z} \right) $$
Calculating each component at the point (2, 0, 3):
- For ( x ):
$$ \frac{\partial V^2}{\partial x} = 2xy^2 + 2xz^2 = 2(2)(0^2) + 2(2)(3^2) = 0 + 2(2)(9) = 36 $$
- For ( y ):
$$ \frac{\partial V^2}{\partial y} = 2y(x^2 + z^2) = 2(0)((2)^2 + (3)^2) = 0 $$
- For ( z ):
$$ \frac{\partial V^2}{\partial z} = 2z(y^2 + x^2) = 2(3)(0^2 + 2^2) = 2(3)(4) = 24 $$
Thus:
$$ \nabla V^2(2, 0, 3) = (36, 0, 24) $$
- Find the Outward Normal to the Sphere
The equation of the sphere is:
$$ x^2 + y^2 + z^2 = 14 $$
The outward normal vector to the surface at a point ( (3, 2, 1) ) is given by:
$$ \mathbf{N} = \nabla(x^2 + y^2 + z^2) = (2x, 2y, 2z) $$
At the point (3, 2, 1):
$$ \mathbf{N} = (2(3), 2(2), 2(1)) = (6, 4, 2) $$
- Normalize the Normal Vector
To find the unit normal vector, we normalize ( \mathbf{N} ):
$$ |\mathbf{N}| = \sqrt{6^2 + 4^2 + 2^2} = \sqrt{36 + 16 + 4} = \sqrt{56} = 2\sqrt{14} $$
Thus:
$$ \mathbf{u} = \frac{1}{|\mathbf{N}|} \mathbf{N} = \left( \frac{6}{2\sqrt{14}}, \frac{4}{2\sqrt{14}}, \frac{2}{2\sqrt{14}} \right) = \left( \frac{3}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{1}{\sqrt{14}} \right) $$
- Calculate the Directional Derivative
The directional derivative in the direction of ( \mathbf{u} ) is given by:
$$ D_{\mathbf{u}} V^2 = \nabla V^2 \cdot \mathbf{u} $$
Calculating the dot product:
$$ D_{\mathbf{u}} V^2 = (36, 0, 24) \cdot \left( \frac{3}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{1}{\sqrt{14}} \right) $$
This yields:
$$ D_{\mathbf{u}} V^2 = 36 \cdot \frac{3}{\sqrt{14}} + 0 \cdot \frac{2}{\sqrt{14}} + 24 \cdot \frac{1}{\sqrt{14}} $$
Simplifying:
$$ D_{\mathbf{u}} V^2 = \frac{108 + 24}{\sqrt{14}} = \frac{132}{\sqrt{14}} $$
- Final Simplification
To express it neatly:
$$ D_{\mathbf{u}} V^2 = \frac{66}{7} \sqrt{14} $$
The directional derivative is:
$$ \frac{66}{7} \sqrt{14} $$
More Information
The directional derivative measures how the function ( V^2 ) changes at a specific point as we move in a particular direction. Finding the gradient helps us understand the rate of change, and the normalization ensures we are considering the direction rather than the magnitude.
Tips
- Forgetting to normalize the normal vector: Always ensure you're using a unit vector for proper directional derivatives.
- Miscalculating the partial derivatives: Double-check calculations especially when using the product rule.
AI-generated content may contain errors. Please verify critical information