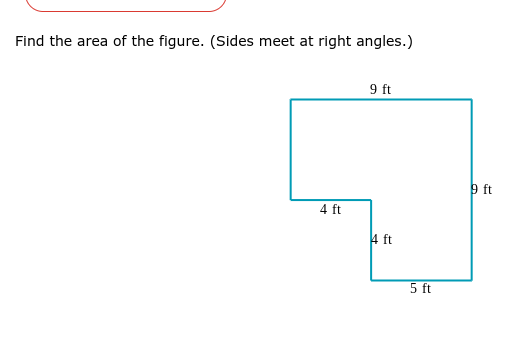
Find the area of the figure. (Sides meet at right angles.)
Understand the Problem
The question is asking to calculate the area of a figure composed of right angles, which involves finding the dimensions and applying the appropriate area formulas for the shapes involved.
Answer
The area of the figure is $$ 61 \, \text{ft}^2 $$.
Answer for screen readers
The area of the figure is $$ 61 , \text{ft}^2 $$.
Steps to Solve
- Identify the shapes and dimensions
The figure is composed of a large rectangle and a small rectangular cutout. The dimensions are:
- Large rectangle: 9 ft (height) and 9 ft (width)
- Small rectangle (cutout): 4 ft (height) and 5 ft (width)
- Calculate the area of the large rectangle
The area of a rectangle is calculated using the formula:
$$ \text{Area} = \text{width} \times \text{height} $$
For the large rectangle:
$$ \text{Area}_{\text{large}} = 9 , \text{ft} \times 9 , \text{ft} = 81 , \text{ft}^2 $$
- Calculate the area of the small rectangle (cutout)
Using the same area formula for the small rectangle:
$$ \text{Area}_{\text{small}} = 5 , \text{ft} \times 4 , \text{ft} = 20 , \text{ft}^2 $$
- Calculate the total area of the figure
To find the total area of the figure, subtract the area of the small rectangle from the area of the large rectangle:
$$ \text{Total Area} = \text{Area}{\text{large}} - \text{Area}{\text{small}} $$
Substituting the areas calculated:
$$ \text{Total Area} = 81 , \text{ft}^2 - 20 , \text{ft}^2 = 61 , \text{ft}^2 $$
The area of the figure is $$ 61 , \text{ft}^2 $$.
More Information
This area represents the net space of the figure after accounting for the cutout section. Such problems are common in geometry where complex shapes need to be simplified into basic ones for area calculation.
Tips
- Forgetting to subtract the area of the cutout from the area of the larger rectangle.
- Miscalculating the dimensions of the rectangles, particularly when side lengths are mixed up.
AI-generated content may contain errors. Please verify critical information