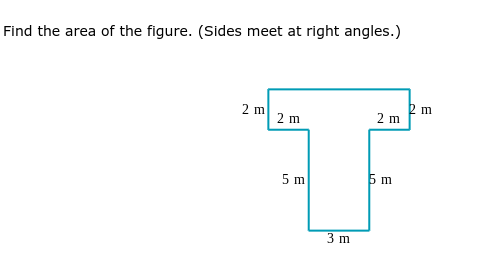
Find the area of the figure. (Sides meet at right angles.)
Understand the Problem
The question is asking for the area calculation of a specific geometric figure, which resembles a 'T' shape made up of various rectangles. To solve it, we will need to break down the figure into identifiable rectangular components and sum their areas.
Answer
The area of the figure is \(23 \, \text{m}^2\).
Answer for screen readers
The area of the figure is (23 , \text{m}^2).
Steps to Solve
-
Identify the rectangular sections The 'T' shape can be broken down into two rectangles: one horizontal on top and one vertical in the center.
-
Calculate the area of the top rectangle The dimensions of the top rectangle are 4 m wide (2 m + 2 m) and 2 m high. The area of the top rectangle is: $$ \text{Area}_{\text{top}} = \text{width} \times \text{height} = 4 , \text{m} \times 2 , \text{m} = 8 , \text{m}^2 $$
-
Calculate the area of the bottom rectangle The dimensions of the bottom rectangle are 3 m wide and 5 m high. The area of the bottom rectangle is: $$ \text{Area}_{\text{bottom}} = \text{width} \times \text{height} = 3 , \text{m} \times 5 , \text{m} = 15 , \text{m}^2 $$
-
Sum the areas of both rectangles To find the total area of the 'T' shape, add the area of the top rectangle and the area of the bottom rectangle: $$ \text{Total Area} = \text{Area}{\text{top}} + \text{Area}{\text{bottom}} = 8 , \text{m}^2 + 15 , \text{m}^2 = 23 , \text{m}^2 $$
The area of the figure is (23 , \text{m}^2).
More Information
The area calculation of composite shapes often involves breaking them into simpler geometric figures. In this case, rectangles were used, which are easier to measure and calculate.
Tips
- Forgetting to sum the areas of all sections of the shape.
- Miscalculating the dimensions of the rectangles.
- Overlooking the proper addition of units when summing areas.
AI-generated content may contain errors. Please verify critical information