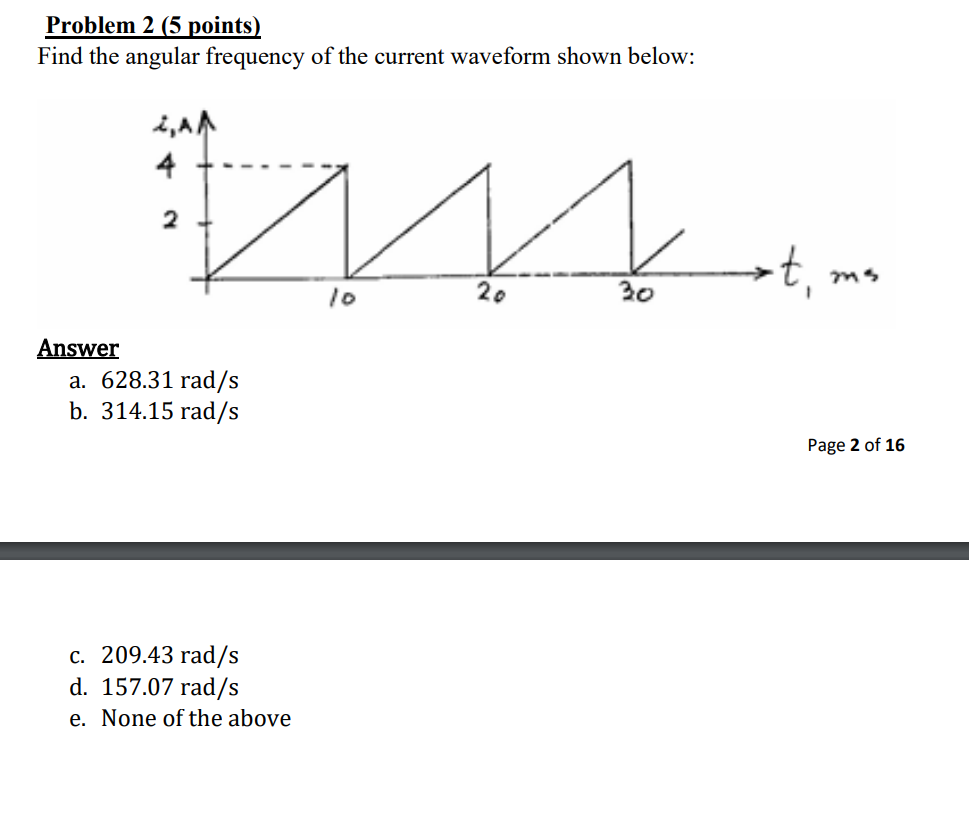
Find the angular frequency of the current waveform shown below.
Understand the Problem
The question is asking to find the angular frequency of a specific current waveform displayed in the attached diagram. To solve this, we need to analyze the waveform, determine its period, and then calculate the angular frequency using the formula ω = 2π/T.
Answer
The angular frequency is approximately $209.44 \text{ rad/s}$.
Answer for screen readers
The angular frequency is approximately $\omega \approx 209.44 \text{ rad/s}$.
Steps to Solve
- Determine the period of the waveform
From the waveform, observe that it repeats every 30 ms. This is the duration of one complete cycle.
- Convert the period to seconds
Convert 30 ms to seconds: $$ T = 30 \text{ ms} = 30 \times 10^{-3} \text{ s} = 0.030 \text{ s} $$
- Calculate the angular frequency
Use the formula for angular frequency: $$ \omega = \frac{2\pi}{T} $$ Substituting the period: $$ \omega = \frac{2\pi}{0.030} \approx 209.44 \text{ rad/s} $$
The angular frequency is approximately $\omega \approx 209.44 \text{ rad/s}$.
More Information
The angular frequency ($\omega$) represents how rapidly the waveform cycles through its period, which is crucial in determining the behavior of alternating currents in circuits.
Tips
- Not converting milliseconds to seconds: Always ensure the units are consistent when calculating periods.
- Misreading the waveform's period: Carefully identify the points at which the waveform completes one cycle.
AI-generated content may contain errors. Please verify critical information