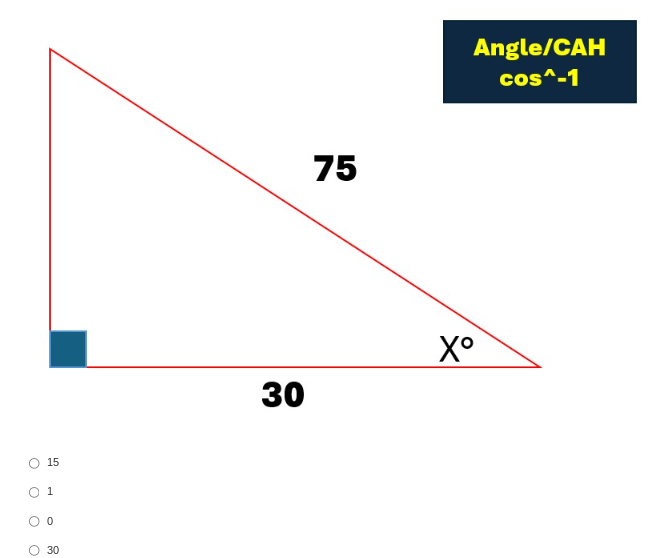
Find the angle X in a right triangle given the adjacent side is 30 and the hypotenuse is 75.
Understand the Problem
The question is asking to find the angle X in a right triangle using the cosine function. Given the lengths of the adjacent side (30) and the hypotenuse (75), we can use the cosine inverse function to calculate X.
Answer
The angle \( X \) is approximately \( 66.42^\circ \).
Answer for screen readers
The angle ( X ) is approximately ( 66.42^\circ ).
Steps to Solve
- Identify the cosine formula
The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. The formula is: $$ \cos(X) = \frac{\text{adjacent}}{\text{hypotenuse}} $$
- Substitute the known values
In this triangle, the adjacent side is 30 and the hypotenuse is 75. Substitute these values into the cosine formula: $$ \cos(X) = \frac{30}{75} $$
- Calculate the cosine value
Simplifying the fraction gives: $$ \cos(X) = \frac{2}{5} $$
- Use the cosine inverse to find the angle
To find angle $X$, you will use the inverse cosine function: $$ X = \cos^{-1}\left(\frac{2}{5}\right) $$
- Calculate the angle using a calculator
Using a scientific calculator or an appropriate software tool: $$ X \approx 66.42^\circ $$
The angle ( X ) is approximately ( 66.42^\circ ).
More Information
In a right triangle, the cosine function allows us to determine angles based on the side ratios. Knowing just two sides can easily help derive the angle using trigonometric identities.
Tips
- Forgetting to use the inverse cosine function after finding the cosine value.
- Miscalculating the fraction, which leads to the wrong cosine value.
- Not using a calculator that is in degree mode when calculating the angle.
AI-generated content may contain errors. Please verify critical information