Find the angle between two circles x^2 + y^2 + x + y = 0 and x^2 + y^2 - x + y = 0.
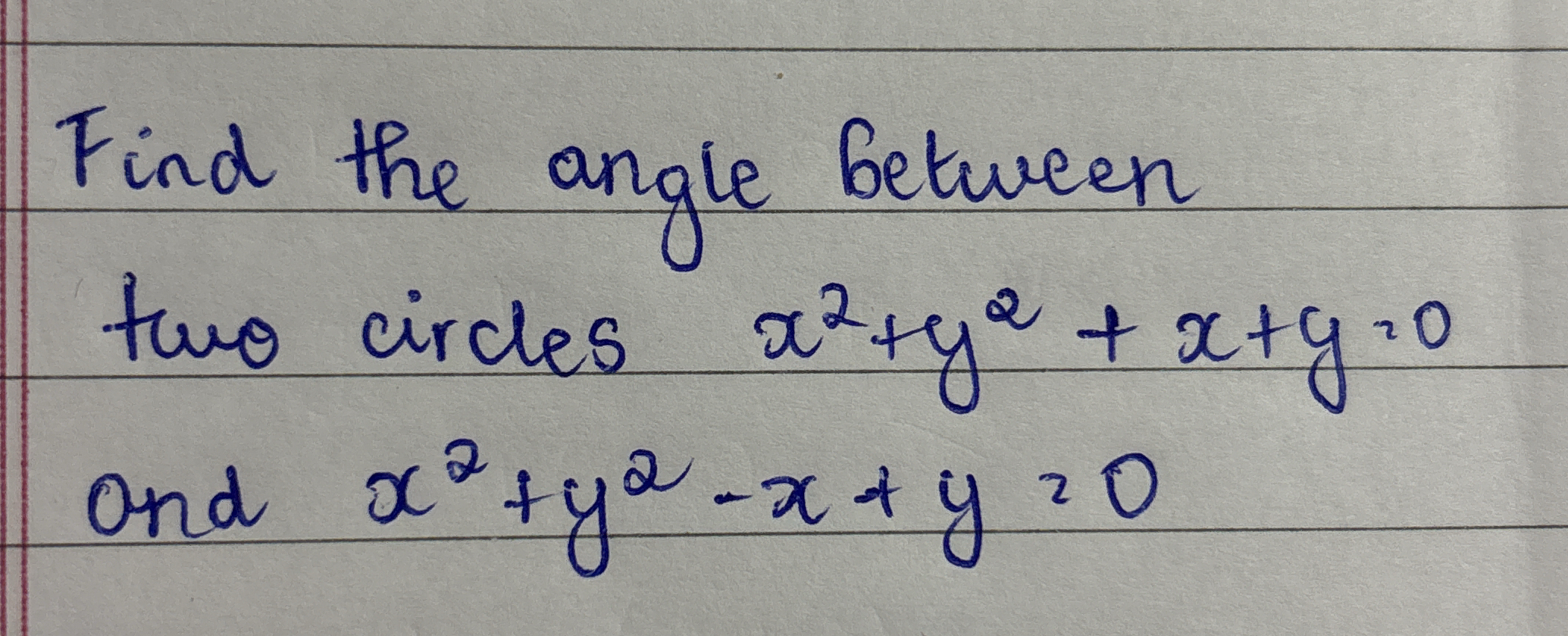
Understand the Problem
The question is asking to find the angle between two circles defined by their equations. This involves determining the geometric relationship between the two circles represented by the given equations.
Answer
$0^\circ$ or $180^\circ$
Answer for screen readers
The angle between the two circles is $0^\circ$ or $180^\circ$.
Steps to Solve
- Rewrite the equations in standard form
To find the centers of the circles, rewrite the circle equations in standard form.
The first circle equation is: $$ x^2 + y^2 + x + y = 0 $$ We can complete the square for both $x$ and $y$:
-
For $x$: $$ x^2 + x = (x + \frac{1}{2})^2 - \frac{1}{4} $$
-
For $y$: $$ y^2 + y = (y + \frac{1}{2})^2 - \frac{1}{4} $$
Thus, the first circle's equation becomes: $$ (x + \frac{1}{2})^2 + (y + \frac{1}{2})^2 = \frac{1}{2} $$
The center of the first circle is $(-\frac{1}{2}, -\frac{1}{2})$ with a radius of $\frac{1}{\sqrt{2}}$.
The second circle equation is: $$ x^2 + y^2 - x + y = 0 $$
Completing the square:
-
For $x$: $$ x^2 - x = (x - \frac{1}{2})^2 - \frac{1}{4} $$
-
For $y$: $$ y^2 + y = (y + \frac{1}{2})^2 - \frac{1}{4} $$
Thus, the second circle's equation becomes: $$ (x - \frac{1}{2})^2 + (y + \frac{1}{2})^2 = \frac{1}{2} $$
The center of the second circle is $(\frac{1}{2}, -\frac{1}{2})$ with a radius of $\frac{1}{\sqrt{2}}$.
- Find the direction vectors
Next, we determine the direction vectors from the centers of the two circles.
-
For the first circle (center at $(-\frac{1}{2}, -\frac{1}{2})$): We can use the vector pointing right towards the second circle's center: $$ v_1 = \left(\frac{1}{2} - (-\frac{1}{2}), -\frac{1}{2} - (-\frac{1}{2})\right) = (1, 0) $$
-
For the second circle (center at $(\frac{1}{2}, -\frac{1}{2})$): The vector pointing left towards the first circle's center: $$ v_2 = \left(-\frac{1}{2} - \frac{1}{2}, -\frac{1}{2} - (-\frac{1}{2})\right) = (-1, 0) $$
- Calculate the angle between the circles
The angle between the two tangents at the point of intersection can be calculated using the formula: $$ \tan \theta = \left| \frac{m_1 - m_2}{1 + m_1 m_2} \right| $$,
where $m_1$ and $m_2$ are the slopes of the tangent lines at the intersection points.
Here, the slopes are both horizontal, so:
$$ m_1 = 0, \quad m_2 = 0 $$
The angle $\theta$ is thus vertical, and since both tangents are parallel: $$ \theta = 0 $$
Thus, the angle between the circles is either 0 or 180 degrees.
The angle between the two circles is $0^\circ$ or $180^\circ$.
More Information
The angle being $0^\circ$ indicates that the two circles are touching; they share a common tangent. The fact that both have horizontal slopes implies they are parallel in tangent direction at the point of intersection.
Tips
- Forgetting to complete the square correctly when converting the equations of the circles into standard form.
- Confusing the angle between the circles with the angle of intersection which refers simply to their tangent lines.
AI-generated content may contain errors. Please verify critical information