Find all real and imaginary solutions to the equation 4x^3 - 7x^2 - 16x + 28 = 0.
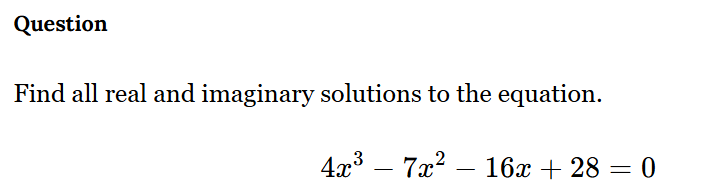
Understand the Problem
The question is asking us to find both real and imaginary solutions for the cubic equation given. This involves factors or finding roots of the polynomial equation using appropriate mathematical methods.
Answer
The solutions are \( x = 2, \frac{7}{4}, -2 \).
Answer for screen readers
The solutions are: ( x = 2, \frac{7}{4}, -2 ).
Steps to Solve
- Set up the equation
We are given the cubic equation:
$$ 4x^3 - 7x^2 - 16x + 28 = 0 $$
- Find Rational Roots
Use the Rational Root Theorem to identify possible rational roots. The factors of the constant term (28) are:
$$ \pm 1, \pm 2, \pm 4, \pm 7, \pm 14, \pm 28 $$
And the factors of the leading coefficient (4) are:
$$ \pm 1, \pm 2, \pm 4 $$
The possible rational roots are the ratios of these factors.
- Test possible roots
We can test some possible rational roots. Let's test ( x = 2 ): $$ 4(2)^3 - 7(2)^2 - 16(2) + 28 = 4(8) - 7(4) - 32 + 28 $$ $$ = 32 - 28 - 32 + 28 = 0 $$ Therefore, ( x = 2 ) is a root.
- Perform synthetic division
Now, use synthetic division to divide the polynomial by ( x - 2 ):
2 | 4 -7 -16 28
| 8 2 -28
---------------------
4 1 -14 0
The quotient is:
$$ 4x^2 + x - 14 $$
- Factor or use the quadratic formula on the quotient
Next, we need to solve:
$$ 4x^2 + x - 14 = 0 $$
Using the quadratic formula where ( a = 4, b = 1, c = -14 ):
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Calculating the discriminant:
$$ b^2 - 4ac = 1^2 - 4(4)(-14) = 1 + 224 = 225 $$
Now plug this into the formula:
$$ x = \frac{-1 \pm \sqrt{225}}{2(4)} = \frac{-1 \pm 15}{8} $$
- Calculate the roots
Calculating the two roots:
-
For ( +15 ): $$ x = \frac{14}{8} = \frac{7}{4} $$
-
For ( -15 ): $$ x = \frac{-16}{8} = -2 $$
- Summary of the solutions
The solutions to the original equation are:
- Real solutions: ( x = 2, \frac{7}{4}, -2 )
- No imaginary solutions since all roots are real.
The solutions are: ( x = 2, \frac{7}{4}, -2 ).
More Information
This cubic equation was solved using the Rational Root Theorem and the quadratic formula, leading to all real solutions. Cubic equations can often have one real root and two complex roots, but in this case, all roots are real.
Tips
- Forgetting to check the discriminant when using the quadratic formula can lead to errors in identifying roots.
- Not testing all possible rational roots might miss out on identifying a root initially.
AI-generated content may contain errors. Please verify critical information