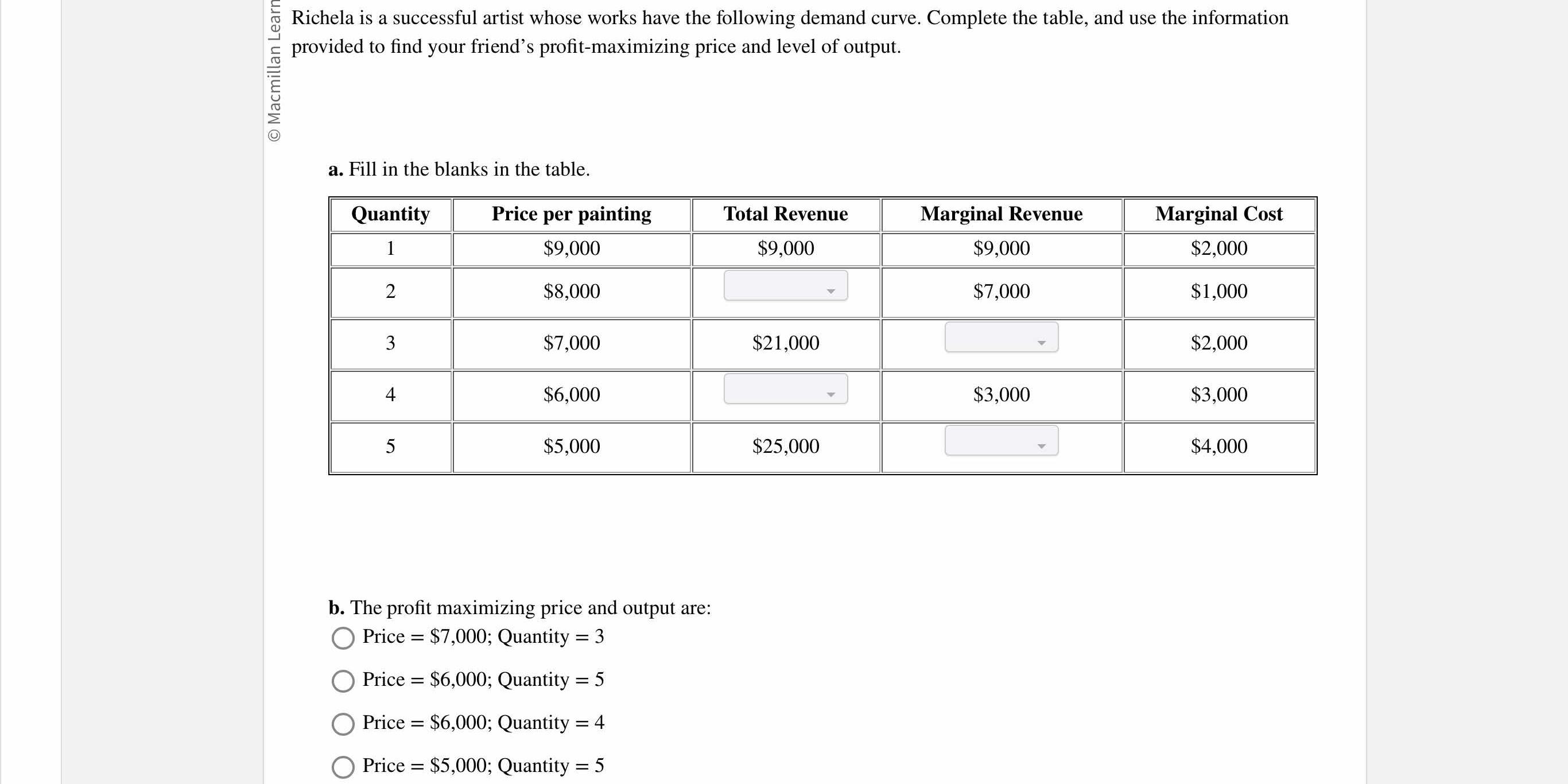
Fill in the blanks in the table.
Understand the Problem
The question is asking to fill in a table related to a demand curve for a painter's work, including calculating total revenue and marginal revenue based on given quantities and prices.
Answer
Price = $6,000; Quantity = 4
Answer for screen readers
The profit-maximizing price and output are: Price = $6,000; Quantity = 4.
Steps to Solve
- Calculate Total Revenue for Each Quantity Total Revenue (TR) is calculated by multiplying the price per painting by the quantity.
-
For 1 painting at $9,000: $$ TR_1 = 9,000 \times 1 = 9,000 $$
-
For 2 paintings at $8,000: $$ TR_2 = 8,000 \times 2 = 16,000 $$
-
For 3 paintings at $7,000: $$ TR_3 = 7,000 \times 3 = 21,000 $$
-
For 4 paintings at $6,000: $$ TR_4 = 6,000 \times 4 = 24,000 $$
-
For 5 paintings at $5,000: $$ TR_5 = 5,000 \times 5 = 25,000 $$
- Calculate Marginal Revenue Marginal Revenue (MR) is the change in Total Revenue for one additional unit sold.
-
For the 2nd painting: $$ MR_2 = TR_2 - TR_1 = 16,000 - 9,000 = 7,000 $$
-
For the 3rd painting: $$ MR_3 = TR_3 - TR_2 = 21,000 - 16,000 = 5,000 $$
-
For the 4th painting: $$ MR_4 = TR_4 - TR_3 = 24,000 - 21,000 = 3,000 $$
-
For the 5th painting: $$ MR_5 = TR_5 - TR_4 = 25,000 - 24,000 = 1,000 $$
- Fill in the table Using the calculated values, fill in the table.
| Quantity | Price per painting | Total Revenue | Marginal Revenue | Marginal Cost |
|---|---|---|---|---|
| 1 | $9,000 | $9,000 | $9,000 | $2,000 |
| 2 | $8,000 | $16,000 | $7,000 | $1,000 |
| 3 | $7,000 | $21,000 | $5,000 | $2,000 |
| 4 | $6,000 | $24,000 | $3,000 | $3,000 |
| 5 | $5,000 | $25,000 | $1,000 | $4,000 |
- Identify the profit-maximizing output The profit-maximizing output occurs where Marginal Revenue equals Marginal Cost.
From the values:
- For 3 paintings, MR ($5,000) is greater than MC ($2,000)
- For 4 paintings, MR ($3,000) is greater than MC ($3,000)
- For 5 paintings, MR ($1,000) is less than MC ($4,000)
Thus, the profit-maximizing quantity is 4 paintings, at a price of $6,000.
The profit-maximizing price and output are: Price = $6,000; Quantity = 4.
More Information
This analysis uses the concept of marginal analysis, where firms maximize profit by producing up to the point where marginal revenue equals marginal cost. Understanding this framework is crucial for pricing strategies in economics.
Tips
- Mistake in calculating Total Revenue by not multiplying correctly.
- Confusing Marginal Revenue with Total Revenue.
- Not correctly identifying the profit-maximizing output by neglecting to compare MR and MC.
AI-generated content may contain errors. Please verify critical information