Factor 3n^7 - 75n^5 completely.
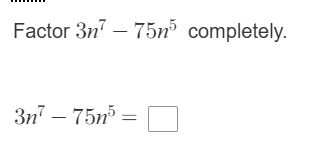
Understand the Problem
The question is asking to factor the expression 3n⁷ - 75n⁵ completely. This involves finding common factors and possibly using factoring techniques such as taking out the greatest common factor.
Answer
The factorization of the expression is: $$ 3n^5(n - 5)(n + 5) $$
Answer for screen readers
The expression factored completely is:
$$ 3n^5(n - 5)(n + 5) $$
Steps to Solve
- Identify the Greatest Common Factor (GCF)
First, identify the GCF of the coefficients and the variable parts of the expression. The coefficients are 3 and -75. The GCF is 3. For the variable part $n^7$ and $n^5$, the GCF is $n^5$.
So, the GCF for the entire expression is $3n^5$.
- Factor out the GCF
Next, factor out the GCF from the expression:
$$ 3n^7 - 75n^5 = 3n^5(n^2 - 25) $$
- Recognize the Difference of Squares
Observe that the expression $n^2 - 25$ is a difference of squares, which can be factored further. Recall that:
$$ a^2 - b^2 = (a - b)(a + b) $$
Here, $a = n$ and $b = 5$.
- Apply the Difference of Squares
Now, apply the difference of squares formula to factor $n^2 - 25$:
$$ n^2 - 25 = (n - 5)(n + 5) $$
- Combine the Factors
Now, combine everything back together:
$$ 3n^7 - 75n^5 = 3n^5(n - 5)(n + 5) $$
The expression factored completely is:
$$ 3n^5(n - 5)(n + 5) $$
More Information
Factoring expressions is a key skill in algebra that allows simplification and solving of equations. Understanding the difference of squares is particularly useful for factoring polynomial expressions.
Tips
- Forgetting to find and factor out the GCF before applying other techniques.
- Not recognizing the difference of squares, which can lead to an incomplete factorization.
- Neglecting to simplify the expression after factoring.
AI-generated content may contain errors. Please verify critical information