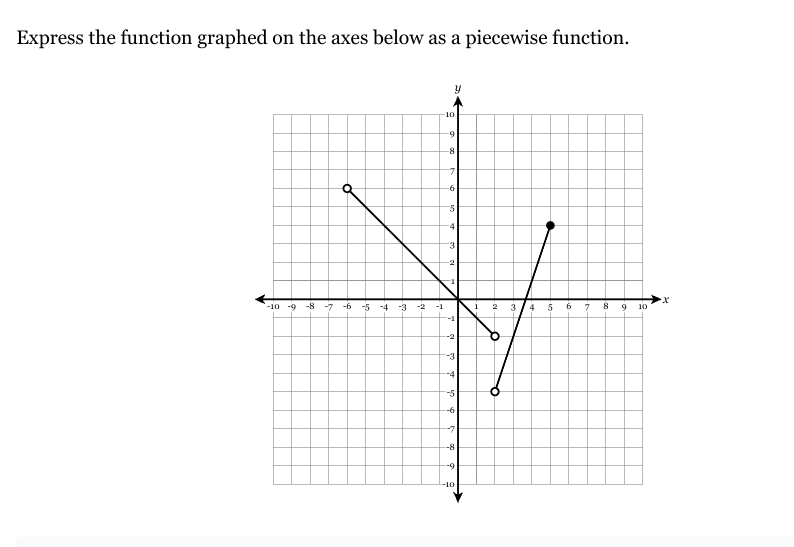
Express the function graphed on the axes below as a piecewise function.

Steps to Solve

1. Identify the intervals for the function segments

Review the graph to identify the intervals on the x-axis where the function changes. The function consists of three main segments:

• From $x = -10$ to $x = -2$
• From $x = -2$ to $x = 4$
• From $x = 4$ to $x = 10$

2. Determine the equations for each segment

Next, find the equations that describe the function for each of these intervals:

• Segment 1 ($-10 \leq x < -2$): This segment is linear with endpoints $(-10, 5)$ and $(-2, -3)$.

  The slope $m$ can be calculated: $$ m = \frac{-3 - 5}{-2 + 10} = \frac{-8}{8} = -1 $$ The line equation in point-slope form using $(-2, -3)$: $$ y + 3 = -1(x + 2) $$ Simplifying gives: $$ y = -x - 1 $$

• Segment 2 ($-2 \leq x < 4$): This segment also is linear with endpoints $(-2, -3)$ and $(4, 7)$.

  The slope $m$ again: $$ m = \frac{7 - (-3)}{4 - (-2)} = \frac{10}{6} = \frac{5}{3} $$ Using point-slope form with $(-2, -3)$: $$ y + 3 = \frac{5}{3}(x + 2) $$ Simplifying gives: $$ y = \frac{5}{3}x + \frac{1}{3} $$

• Segment 3 ($4 \leq x \leq 10$): This segment is linear with endpoints $(4, 7)$ and $(10, -3)$.

  The slope $m$: $$ m = \frac{-3 - 7}{10 - 4} = \frac{-10}{6} = -\frac{5}{3} $$ Using point-slope form with $(4, 7)$: $$ y - 7 = -\frac{5}{3}(x - 4) $$ Simplifying gives: $$ y = -\frac{5}{3}x + \frac{43}{3} $$

3. Write the piecewise function

Now, we can piece it together into one function:

$$ f(x) = \begin{cases} -x - 1 & \text{for } -10 \leq x < -2 \ \frac{5}{3}x + \frac{1}{3} & \text{for } -2 \leq x < 4 \ -\frac{5}{3}x + \frac{43}{3} & \text{for } 4 \leq x \leq 10 \end{cases} $$