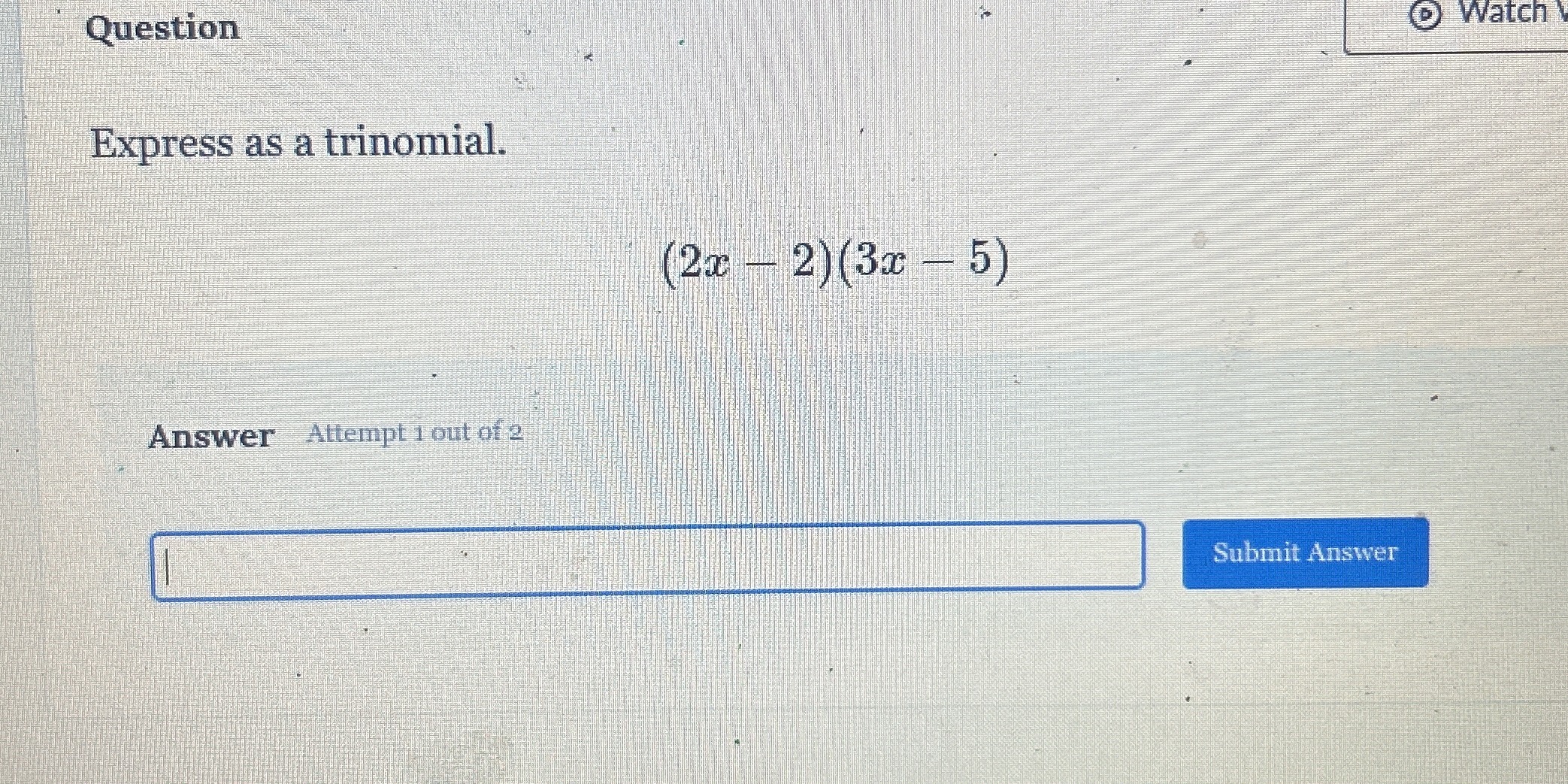
Express as a trinomial: (2x - 2)(3x - 5)

Understand the Problem

The question is asking to express the product of the two binomials (2x - 2)(3x - 5) as a trinomial. This will involve using the distributive property or FOIL method to combine the terms.

Answer

The trinomial is $ 6x^2 - 16x + 10 $.

Steps to Solve

Identify the terms to multiply

We have two binomials: $(2x - 2)$ and $(3x - 5)$.

Use the FOIL method

Apply the FOIL method (First, Outer, Inner, Last) to multiply the binomials.

First: $2x * 3x = 6x^2$
Outer: $2x * (-5) = -10x$
Inner: $(-2) * 3x = -6x$
Last: $(-2) * (-5) = 10$

Combine like terms

Now we will combine the terms from the FOIL process.

The terms are:

$6x^2$
$-10x$ (from Outer)
$-6x$ (from Inner)
$10$ (from Last)

Combine the $x$ terms: $$ -10x - 6x = -16x $$

Write the final trinomial

Putting it all together: $$ 6x^2 - 16x + 10 $$

The product expressed as a trinomial is: ( 6x^2 - 16x + 10 )

More Information

When multiplying binomials, it's important to ensure you apply the distributive property correctly. The FOIL method helps in remembering to multiply all combinations of terms.

Tips

Failing to combine like terms after multiplication.
Misplacing signs while distributing (make sure to keep track of positive and negative signs).

AI-generated content may contain errors. Please verify critical information

Thank you for voting!