Evaluate the summation from n=1 to 11 of (3/4)^n.
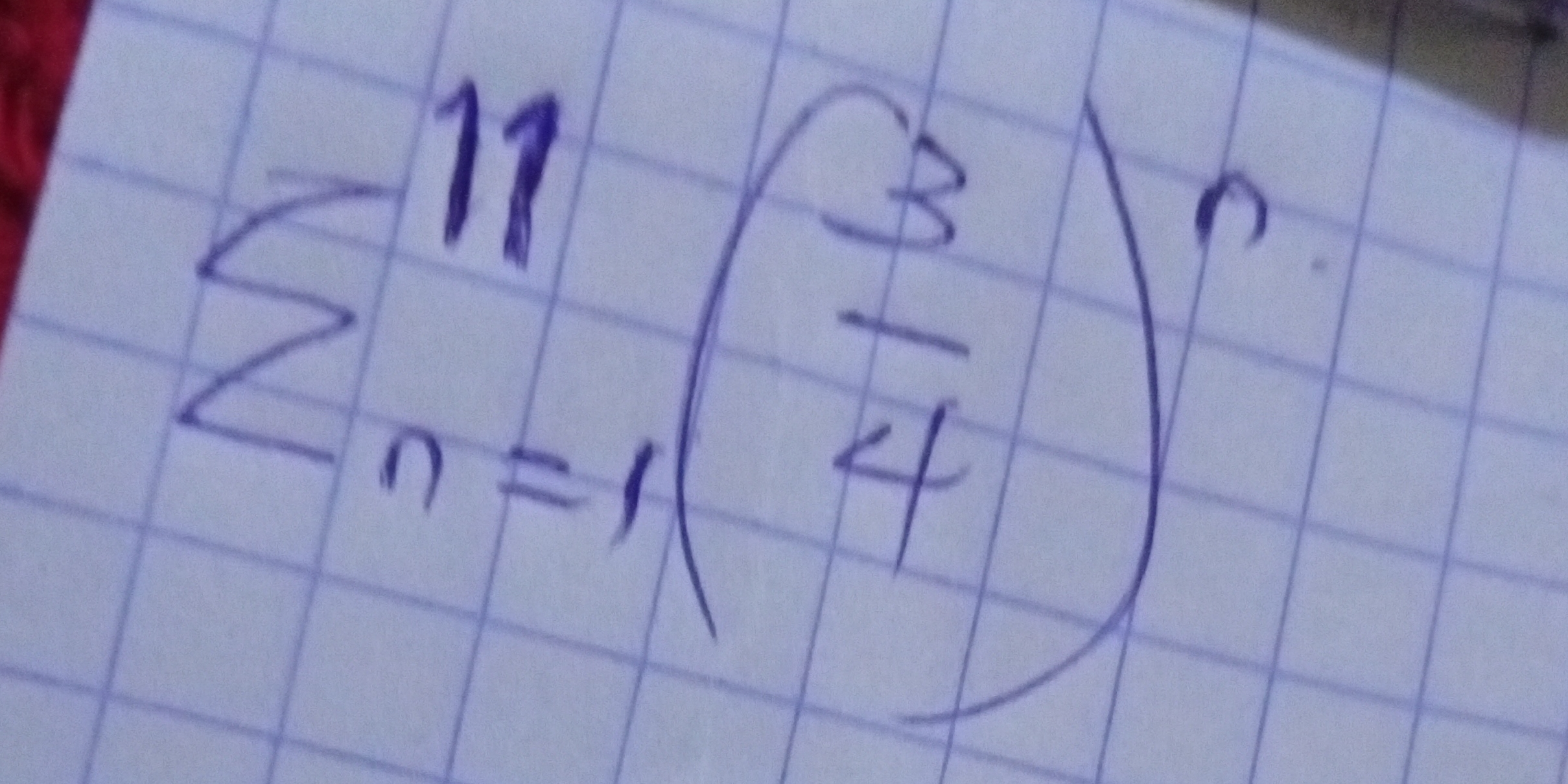
Understand the Problem
The question appears to involve a mathematical summation, specifically the notation for the sum of a series starting from n=1 to 11, combined with a fraction. This requires a mathematical approach to evaluate or simplify the expression given.
Answer
The approximate sum of the series is \( S_{11} \approx 2.905 \).
Answer for screen readers
The approximate sum of the series is ( S_{11} \approx 2.905 ).
Steps to Solve
-
Identify the geometric series parameters The summation given is from $n=1$ to $n=11$ of the expression $\left(\frac{3}{4}\right)^n$. This is a geometric series where:
- The first term ( a = \left(\frac{3}{4}\right)^1 = \frac{3}{4} )
- The common ratio ( r = \frac{3}{4} )
- The number of terms ( n = 11 )
-
Apply the formula for the sum of a geometric series The formula for the sum ( S_n ) of the first ( n ) terms of a geometric series is: $$ S_n = a \frac{1 - r^n}{1 - r} $$ Substituting the identified values:
- ( a = \frac{3}{4} )
- ( r = \frac{3}{4} )
- ( n = 11 )
So we have: $$ S_{11} = \frac{3}{4} \frac{1 - \left(\frac{3}{4}\right)^{11}}{1 - \frac{3}{4}} $$
-
Calculate the denominator The denominator simplifies as follows: $$ 1 - \frac{3}{4} = \frac{1}{4} $$
-
Substitute and simplify the sum Now substituting back into the formula: $$ S_{11} = \frac{3}{4} \frac{1 - \left(\frac{3}{4}\right)^{11}}{\frac{1}{4}} $$ This simplifies to: $$ S_{11} = 3 \left(1 - \left(\frac{3}{4}\right)^{11}\right) $$
-
Calculate (\left(\frac{3}{4}\right)^{11}) We need to compute: $$ \left(\frac{3}{4}\right)^{11} \approx 0.031676352 $$ Now plug this back into the equation: $$ S_{11} = 3 \left(1 - 0.031676352\right) $$
-
Final calculation Compute the final sum: $$ S_{11} = 3 \times (0.968323648) \approx 2.904970944 $$
The approximate sum of the series is ( S_{11} \approx 2.905 ).
More Information
The series represents a geometric sequence, which converges more rapidly as the common ratio approaches 1. In this case, as ( n ) increases, the sum gets closer to the finite limit dictated by the first term and common ratio.
Tips
- Forgetting to adjust the formula for the geometric series or using incorrect bounds.
- Miscalculating the powers or fractions involved in the computations.
- Not recognizing that the common ratio must be less than 1 for the series to converge.
AI-generated content may contain errors. Please verify critical information