Solve the system of equations: x + y = 7 x - y = 3
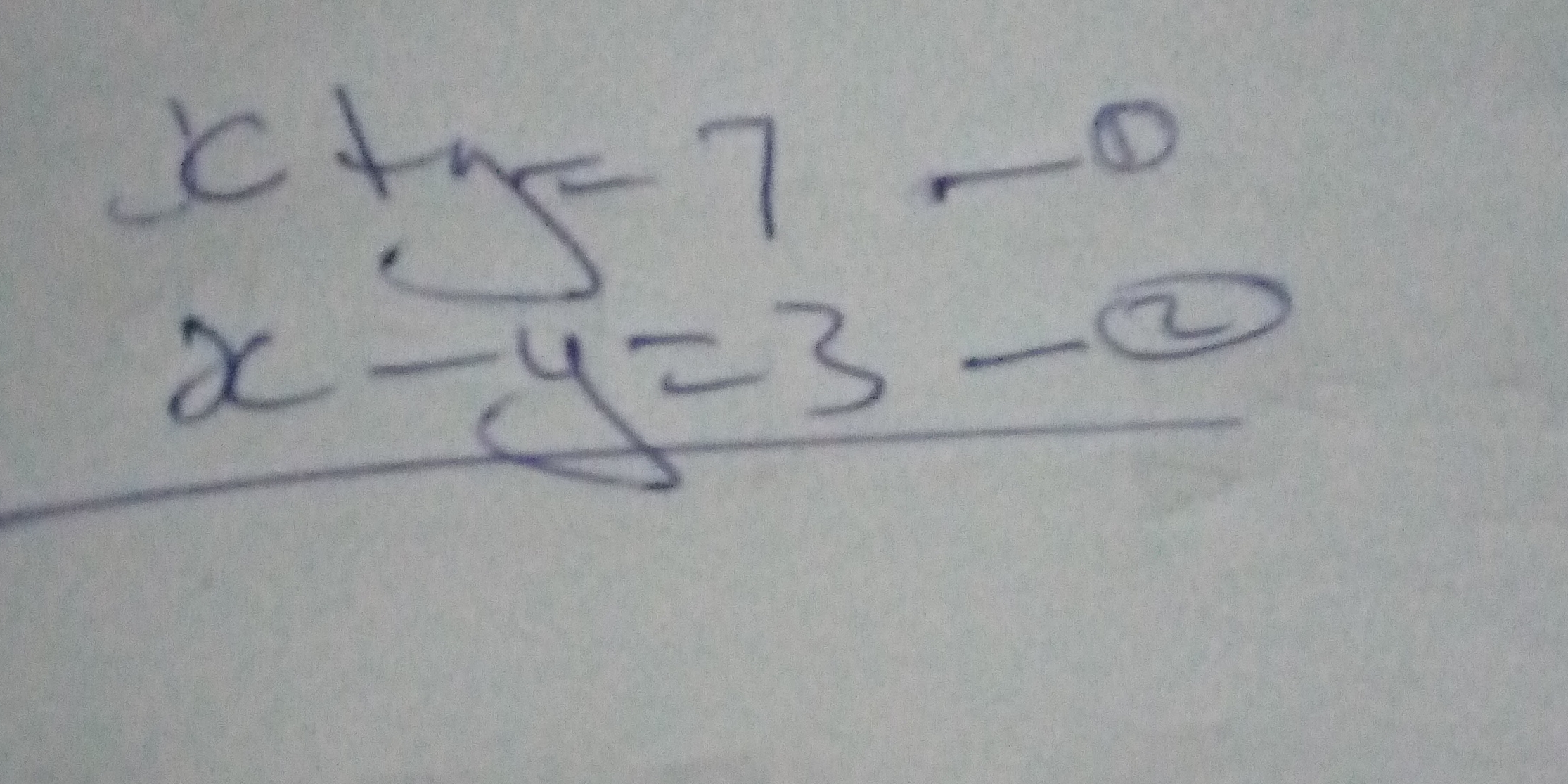
Understand the Problem
The question presents a system of two linear equations with two variables, x and y. The objective is to find the values of x and y that satisfy both equations simultaneously. To solve, we can use methods like substitution, elimination, or matrix operations to find the precise values for both x and y.
Answer
$x = 5$, $y = 2$
Answer for screen readers
$x = 5$ and $y = 2$
Steps to Solve
- Write down the equations
We have: $$ x + y = 7 $$ $$ x - y = 3 $$
- Eliminate $y$ by adding the equations
Adding the two equations eliminates $y$: $$ (x + y) + (x - y) = 7 + 3 $$ $$ 2x = 10 $$
- Solve for $x$
Divide both sides by 2: $$ x = \frac{10}{2} $$ $$ x = 5 $$
- Substitute $x$ back into one of the original equations to solve for $y$
Using the first equation: $$ 5 + y = 7 $$
- Solve for $y$
Subtract 5 from both sides: $$ y = 7 - 5 $$ $$ y = 2 $$
$x = 5$ and $y = 2$
More Information
The point of intersection of the two lines $x + y = 7$ and $x - y = 3$ is $(5, 2)$.
Tips
A common mistake is making an arithmetic error when adding or subtracting the equations, or when substituting the value of one variable back into an equation to solve for the other variable. Always double-check your calculations to avoid these errors.
AI-generated content may contain errors. Please verify critical information