Solve the inequality x^2 + 7x < 0
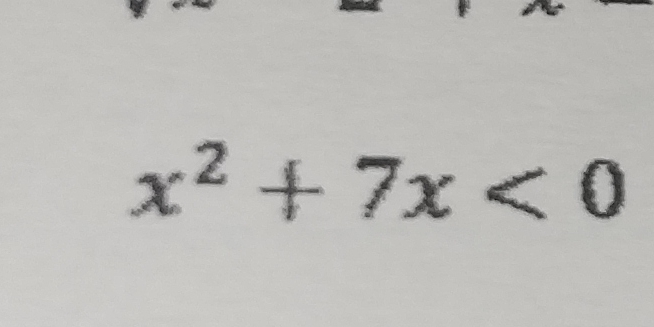
Understand the Problem
The question asks us to solve a quadratic inequality. We need to find the values of x for which the expression x^2 + 7x is less than 0. We can solve this by factoring the expression, finding the critical points, and then testing intervals to determine where the inequality holds true.
Answer
$-7 < x < 0$
Answer for screen readers
$-7 < x < 0$
Steps to Solve
-
Factor the quadratic expression Factor out the common factor $x$ from the expression $x^2 + 7x$: $x(x + 7) < 0$
-
Find the critical points Set each factor equal to zero and solve for $x$ to find the critical points: $x = 0$ and $x + 7 = 0 \implies x = -7$
-
Determine the test intervals The critical points divide the number line into three intervals: $(-\infty, -7)$, $(-7, 0)$, and $(0, \infty)$.
-
Test each interval Choose a test value within each interval and plug it into the factored inequality $x(x + 7) < 0$ to see if the inequality holds true.
-
Interval $(-\infty, -7)$: Test $x = -8$. $(-8)(-8 + 7) = (-8)(-1) = 8 > 0$. The inequality is false.
-
Interval $(-7, 0)$: Test $x = -1$. $(-1)(-1 + 7) = (-1)(6) = -6 < 0$. The inequality is true.
-
Interval $(0, \infty)$: Test $x = 1$. $(1)(1 + 7) = (1)(8) = 8 > 0$. The inequality is false.
-
-
Write the solution Since the inequality is true for the interval $(-7, 0)$, the solution to the inequality is $-7 < x < 0$.
$-7 < x < 0$
More Information
The solution to the inequality $x^2 + 7x < 0$ represents all values of $x$ that make the quadratic expression negative. In this case that is all real numbers between $-7$ and $0$, not including $-7$ and $0$.
Tips
A common mistake is including the endpoints $-7$ and $0$ in the solution. Because the inequality is strict ($<$ and not $\leq$), the endpoints are not included. Another common mistake is incorrectly determining the intervals where the inequality holds true. This can be avoided by carefully testing values in each interval.
AI-generated content may contain errors. Please verify critical information