Evaluate the integral from -1 to 1 of 12x^5 + 12x^2 dx.
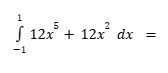
Understand the Problem
The question is asking to evaluate the definite integral of the function 12x^5 + 12x^2 from -1 to 1. This involves finding the antiderivative of the function and then applying the Fundamental Theorem of Calculus.
Answer
The value of the integral is \(8\).
Answer for screen readers
The final answer to the definite integral is (8).
Steps to Solve
- Find the Antiderivative To evaluate the definite integral, we first find the antiderivative of the function (12x^{5} + 12x^{2}).
The antiderivative is calculated as follows: $$ \int (12x^5 + 12x^2) , dx = 12 \cdot \frac{x^6}{6} + 12 \cdot \frac{x^3}{3} + C = 2x^{6} + 4x^{3} + C $$
-
Apply the Fundamental Theorem of Calculus Now we apply the Fundamental Theorem of Calculus, which states that if (F(x)) is an antiderivative of (f(x)), then: $$ \int_{a}^{b} f(x) , dx = F(b) - F(a) $$ In our case, we need to compute (F(1)) and (F(-1)).
-
Calculate (F(1)) and (F(-1)) Substituting the limits into the antiderivative: $$ F(1) = 2(1)^{6} + 4(1)^{3} = 2 + 4 = 6 $$ $$ F(-1) = 2(-1)^{6} + 4(-1)^{3} = 2 - 4 = -2 $$
-
Subtract to Get the Final Answer Now, we subtract (F(-1)) from (F(1)): $$ \int_{-1}^{1} (12x^5 + 12x^2) , dx = F(1) - F(-1) = 6 - (-2) = 6 + 2 = 8 $$
The final answer to the definite integral is (8).
More Information
The integral represents the area under the curve (12x^5 + 12x^2) between the limits (-1) and (1). Since this function is odd (meaning it has symmetry about the origin) for the (x^5) term, its contributions cancel out on that interval but the even (x^2) term contributes positively, resulting in a definite area of (8).
Tips
- Forgetting to consider odd/even functions: Sometimes, students forget the properties of odd and even functions when determining the area.
- Miscalculating the antiderivative: Ensure that you apply the power rule correctly when integrating.
AI-generated content may contain errors. Please verify critical information