Evaluate the following limit: lim (x->1) (x^(1/6) - 1) / (x^(1/3) - 1)
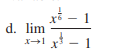
Understand the Problem
The question is asking to evaluate the limit of a rational function as x approaches 1. The function involves fractional exponents, requiring careful manipulation to find the limit. We will need to evaluate the limit. L'Hopital's rule may also be helpful, or algebraic manipulation by factoring.
Answer
$\frac{1}{2}$
Answer for screen readers
$\frac{1}{2}$
Steps to Solve
-
Check for Indeterminate Form First, we check if the limit results in an indeterminate form when we directly substitute $x = 1$. We get $\frac{1^{\frac{1}{6}} - 1}{1^{\frac{1}{3}} - 1} = \frac{1 - 1}{1 - 1} = \frac{0}{0}$, which is an indeterminate form. This means we need to manipulate the expression to evaluate the limit.
-
Apply L'Hopital's Rule Since we have the indeterminate form $\frac{0}{0}$, we can apply L'Hopital's Rule. This involves taking the derivative of the numerator and the derivative of the denominator with respect to $x$.
-
Differentiate the Numerator The derivative of the numerator $x^{\frac{1}{6}} - 1$ with respect to $x$ is: $$ \frac{d}{dx}(x^{\frac{1}{6}} - 1) = \frac{1}{6}x^{\frac{1}{6} - 1} = \frac{1}{6}x^{-\frac{5}{6}} $$
-
Differentiate the Denominator The derivative of the denominator $x^{\frac{1}{3}} - 1$ with respect to $x$ is: $$ \frac{d}{dx}(x^{\frac{1}{3}} - 1) = \frac{1}{3}x^{\frac{1}{3} - 1} = \frac{1}{3}x^{-\frac{2}{3}} $$
-
Apply L'Hopital's Rule and Simplify Now, we apply L'Hopital's Rule: $$ \lim_{x\to 1} \frac{x^{\frac{1}{6}} - 1}{x^{\frac{1}{3}} - 1} = \lim_{x\to 1} \frac{\frac{1}{6}x^{-\frac{5}{6}}}{\frac{1}{3}x^{-\frac{2}{3}}} $$ We simplify the expression: $$ \lim_{x\to 1} \frac{\frac{1}{6}x^{-\frac{5}{6}}}{\frac{1}{3}x^{-\frac{2}{3}}} = \lim_{x\to 1} \frac{1}{6} \cdot \frac{3}{1} \cdot \frac{x^{-\frac{5}{6}}}{x^{-\frac{2}{3}}} = \lim_{x\to 1} \frac{1}{2} x^{-\frac{5}{6} + \frac{2}{3}} = \lim_{x\to 1} \frac{1}{2} x^{-\frac{5}{6} + \frac{4}{6}} = \lim_{x\to 1} \frac{1}{2} x^{-\frac{1}{6}} $$
-
Evaluate the Limit Now, we substitute $x = 1$ into the simplified expression: $$ \lim_{x\to 1} \frac{1}{2} x^{-\frac{1}{6}} = \frac{1}{2} (1)^{-\frac{1}{6}} = \frac{1}{2} \cdot 1 = \frac{1}{2} $$
$\frac{1}{2}$
More Information
The result of the limit is $\frac{1}{2}$. When dealing with indeterminate forms, L'Hopital's rule can be a quick way to find the limit if differentiation is straightforward
Tips
A common mistake is to incorrectly differentiate the numerator or the denominator, particularly with fractional exponents. Additionally, some students may incorrectly simplify the expression after applying L'Hopital's rule. Also, one might forget to check for the indeterminate form before applying L'Hopital's Rule, which is a crucial step.
AI-generated content may contain errors. Please verify critical information