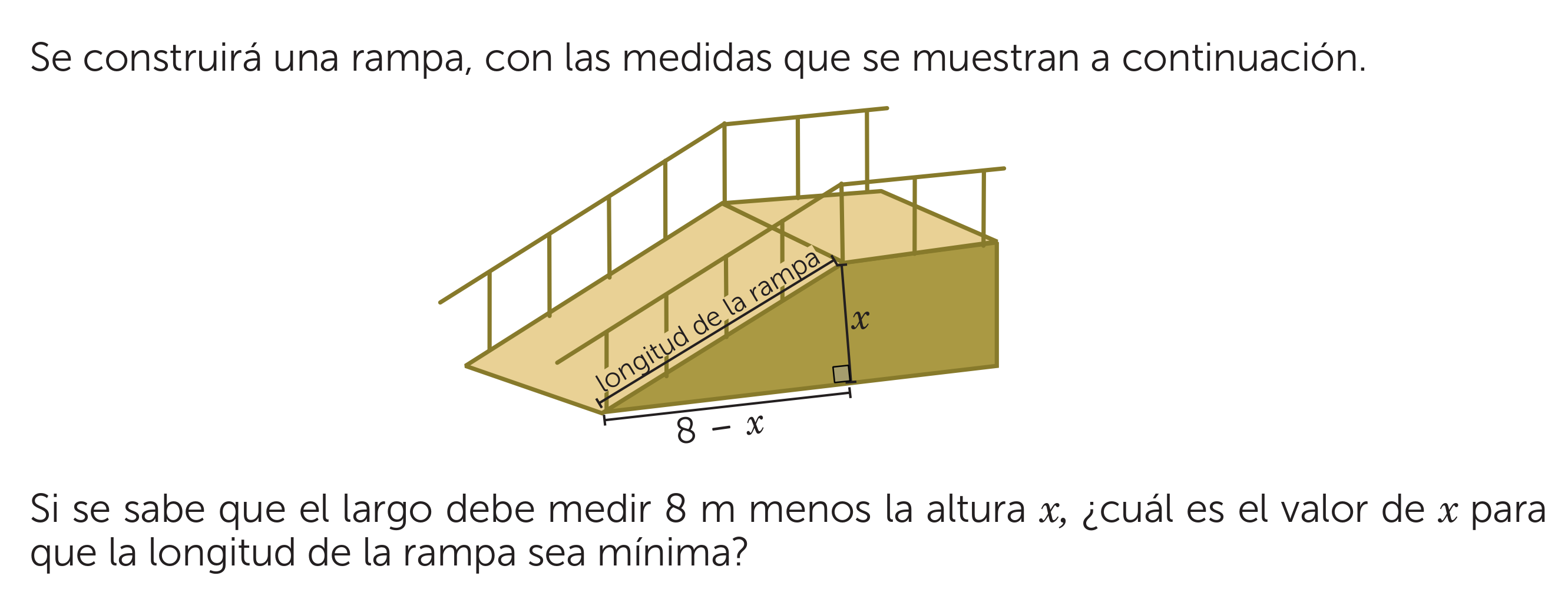
Se construirá una rampa, con las medidas que se muestran a continuación. Si se sabe que el largo debe medir 8 m menos la altura x, ¿cuál es el valor de x para que la longitud de la... Se construirá una rampa, con las medidas que se muestran a continuación. Si se sabe que el largo debe medir 8 m menos la altura x, ¿cuál es el valor de x para que la longitud de la rampa sea mínima? Read more

Steps to Solve

1. Define the length of the ramp using the Pythagorean theorem. The length of the ramp, $L$, is the hypotenuse of a right triangle with legs of length $x$ and $8-x$. Therefore, we have $$L = \sqrt{x^2 + (8-x)^2}$$

2. Simplify the expression for the length of the ramp. Expanding the square, we get $L = \sqrt{x^2 + 64 - 16x + x^2} = \sqrt{2x^2 - 16x + 64}$.

3. Minimize the square of the length. To minimize $L$, it is sufficient to minimize $L^2 = 2x^2 - 16x + 64$. Let $f(x) = 2x^2 - 16x + 64$.

4. Find the critical points of the function $f(x)$. To find the critical points, we compute the derivative of $f(x)$ and set it equal to 0: $f'(x) = 4x - 16$. Setting $f'(x) = 0$, we have $4x - 16 = 0$, which gives $x = 4$.

5. Verify that the critical point is a minimum. To verify that $x=4$ gives a minimum, we compute the second derivative: $f''(x) = 4$. Since $f''(4) = 4 > 0$, we have a minimum at $x=4$.