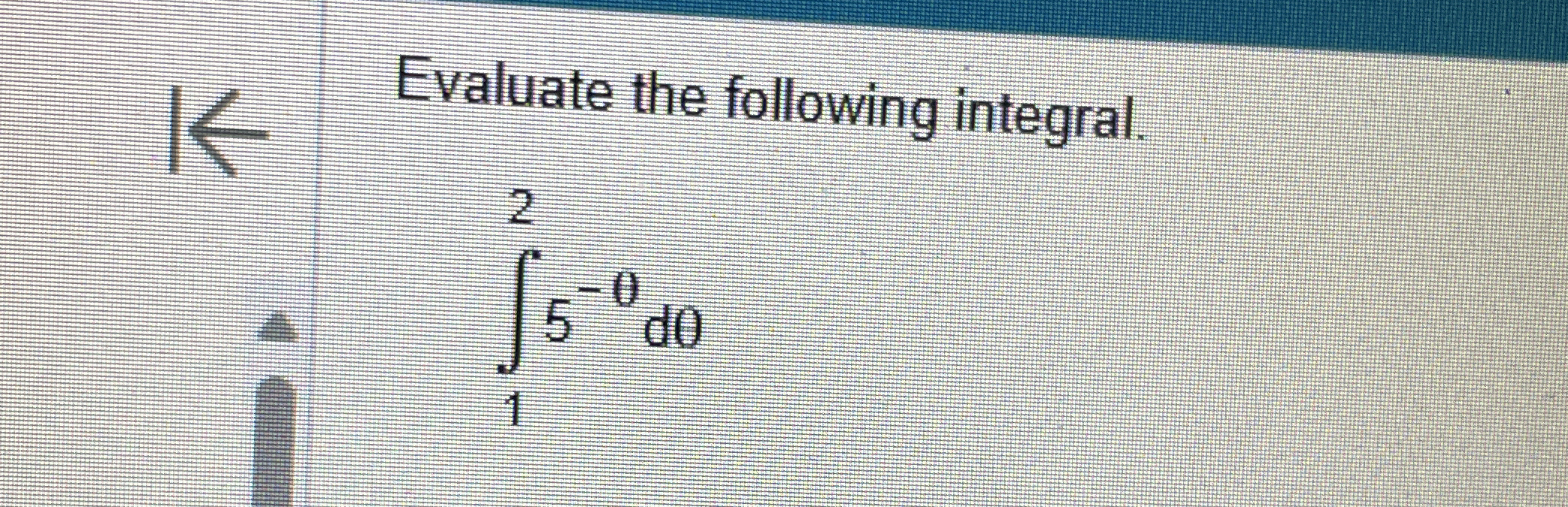
Evaluate the following integral: ∫ from 1 to 2 of 5^(-0) dθ.
Understand the Problem
The question is asking to evaluate a definite integral from 1 to 2 of the function 5 raised to the power of -0.
Answer
The value of the integral is $1$.
Answer for screen readers
The value of the integral is $1$.
Steps to Solve
- Identify the expression inside the integral
The integral we need to evaluate is
$$ \int_1^2 5^{-0} , d\theta $$
Since $-0$ is equal to $0$, we can simplify the expression.
- Simplify the expression
Recognizing that $5^{-0} = 5^0 = 1$, we can rewrite the integral as:
$$ \int_1^2 1 , d\theta $$
- Evaluate the integral
The integral of $1$ with respect to $\theta$ over the interval from $1$ to $2$ is simply the difference between the upper and lower limits:
$$ \int_1^2 1 , d\theta = \theta \bigg|_1^2 = 2 - 1 = 1 $$
The value of the integral is $1$.
More Information
This integral demonstrates the basic principle that the integral of a constant over a given interval results in the constant multiplied by the length of the interval. Since we evaluated the integral of 1 over the interval from 1 to 2, the answer is simply the difference, which is 1.
Tips
- A common mistake is to misinterpret the exponent, thinking $5^{-0}$ is not equal to 1. Remember that any non-zero number raised to the power of 0 is always 1.
- Not recognizing the simplification before proceeding to integrate could lead to unnecessary complications.
AI-generated content may contain errors. Please verify critical information