Evaluate f(x) = (4x + 5x²) / (3x) at x = 1/3.

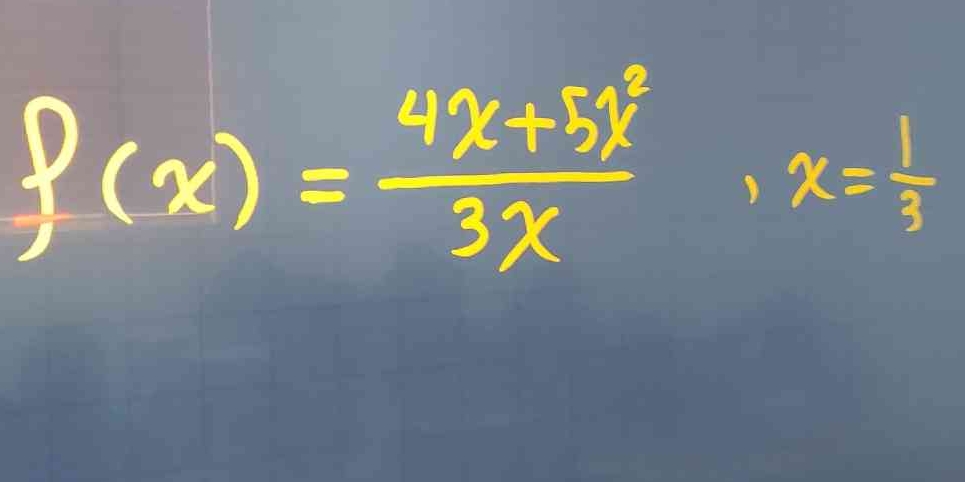
Understand the Problem

The question involves evaluating the function f(x) = (4x + 5x²) / (3x) at the point where x = 1/3. We need to simplify the expression and compute the value.

Answer

The value is $ f\left(\frac{1}{3}\right) = \frac{17}{9} $.

Steps to Solve

Substituting x into the function

Start by substituting ( x = \frac{1}{3} ) into the function:

$$ f\left(\frac{1}{3}\right) = \frac{4\left(\frac{1}{3}\right) + 5\left(\frac{1}{3}\right)^{2}}{3\left(\frac{1}{3}\right)} $$

Calculating the numerator

First, evaluate the expression in the numerator:

$$ 4\left(\frac{1}{3}\right) = \frac{4}{3} $$

For the second term:

$$ 5\left(\frac{1}{3}\right)^{2} = 5 \cdot \frac{1}{9} = \frac{5}{9} $$

So, the numerator becomes:

$$ \frac{4}{3} + \frac{5}{9} $$

Finding a common denominator for the numerator

The common denominator between 3 and 9 is 9. Convert ( \frac{4}{3} ):

$$ \frac{4}{3} = \frac{12}{9} $$

Now, add these two fractions:

$$ \frac{12}{9} + \frac{5}{9} = \frac{17}{9} $$

Calculating the denominator

The denominator is:

$$ 3\left(\frac{1}{3}\right) = 1 $$

Dividing the numerator by the denominator

Now, we can simplify the function:

$$ f\left(\frac{1}{3}\right) = \frac{\frac{17}{9}}{1} = \frac{17}{9} $$

The value of the function at ( x = \frac{1}{3} ) is ( f\left(\frac{1}{3}\right) = \frac{17}{9} ).

More Information

The function ( f(x) ) is a rational function that simplifies when we substitute the value of ( x ). The result ( \frac{17}{9} ) is a non-integer, indicating that the output of the function at this point does not fall on a whole number.

Tips

Confusing the order of operations when substituting the ( x ) value. Always handle numerator and denominator separately.
Forgetting to find a common denominator when adding fractions in the numerator.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!