Evaluate (-36)^(3/2)
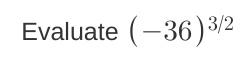
Understand the Problem
The question is asking to evaluate the expression (-36) raised to the power of 3/2. This involves both exponentiation and taking the square root of a negative number.
Answer
The expression evaluates to $-216i$.
Answer for screen readers
The final answer is: $$ -216i $$
Steps to Solve
-
Understand the exponent $3/2$ The exponent $3/2$ can be interpreted as taking the square root and then cubing the result. This can be broken down as: $$ (-36)^{3/2} = \left( (-36)^{1/2} \right)^3 $$
-
Evaluate the square root of a negative number Since $(-36)^{1/2}$ results in an imaginary number, we can express it as: $$ (-36)^{1/2} = \sqrt{-36} = 6i $$ where $i$ is the imaginary unit.
-
Cube the result Now, we need to cube the imaginary number we found: $$ (6i)^3 = 6^3 \cdot i^3 = 216 \cdot (-i) = -216i $$
The final answer is: $$ -216i $$
More Information
This calculation involves understanding complex numbers, as the square root of a negative number leads to the imaginary unit $i$. In mathematical contexts, $i$ is defined as $\sqrt{-1}$, which allows for solutions to polynomial equations that lack real solutions.
Tips
- Not recognizing when to use imaginary numbers can lead to incorrect real-number solutions.
- Forgetting to apply the exponent correctly after taking the root, particularly with negative bases.
AI-generated content may contain errors. Please verify critical information