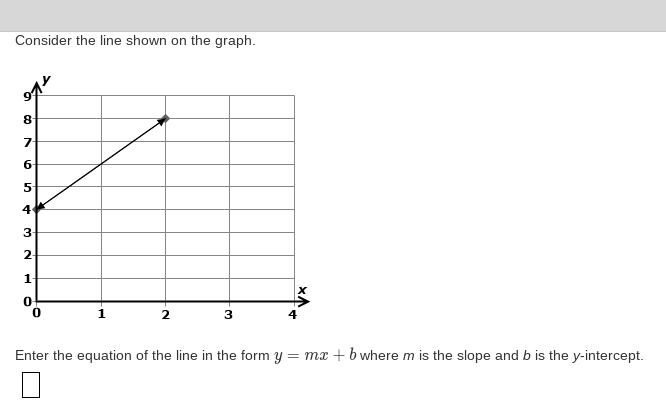
Enter the equation of the line in the form y = mx + b where m is the slope and b is the y-intercept.
Understand the Problem
The question asks for the equation of a straight line shown in a graph, specifically in the slope-intercept form y = mx + b, where m is the slope and b is the y-intercept. This involves analyzing the graph to determine these two parameters.
Answer
The equation of the line is \( y = 2x + 4 \).
Answer for screen readers
The equation of the line is:
$$ y = 2x + 4 $$
Steps to Solve
-
Identify Points on the Line
Look at the graph and identify two points that lie on the line. In this case, the points are (0, 4) and (2, 8).
-
Calculate the Slope (m)
The slope $m$ of a line is calculated using the formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Here, we can plug in our points (0, 4) as $(x_1, y_1)$ and (2, 8) as $(x_2, y_2)$:
$$ m = \frac{8 - 4}{2 - 0} = \frac{4}{2} = 2 $$
-
Determine the Y-Intercept (b)
The y-intercept $b$ is the value of $y$ when $x = 0$. From our identified point (0, 4), we see that:
$$ b = 4 $$
-
Write the Equation of the Line
Using the slope-intercept form $y = mx + b$, we substitute the values of $m$ and $b$ we found:
$$ y = 2x + 4 $$
The equation of the line is:
$$ y = 2x + 4 $$
More Information
The slope of the line is 2, which means for every unit increase in $x$, $y$ increases by 2 units. The y-intercept is at 4, indicating that the line crosses the y-axis at the point (0, 4).
Tips
- Incorrectly identifying points on the line: Ensure the points you choose are exactly on the line.
- Miscalculating the slope: Double-check the slope calculation, especially the difference between the y-coordinates and x-coordinates.
- Forgetting to use the slope-intercept form: Remember to state the final equation in the correct format.
AI-generated content may contain errors. Please verify critical information