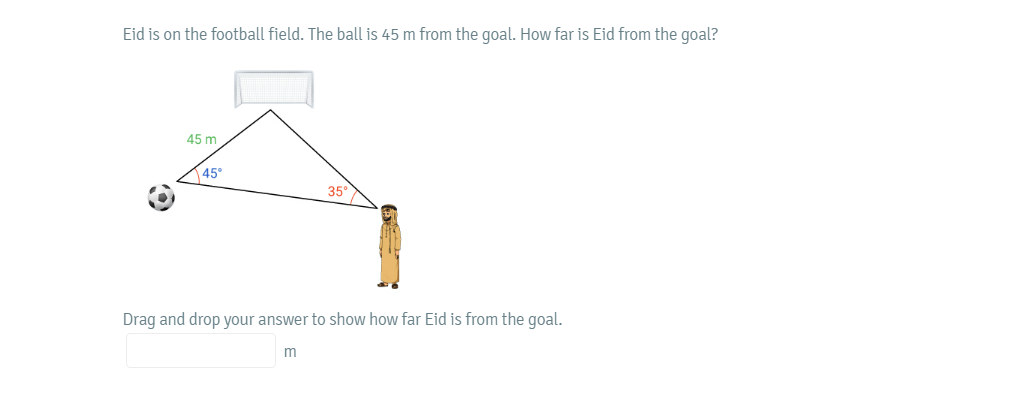
Eid is on the football field. The ball is 45 m from the goal. How far is Eid from the goal?

Steps to Solve

1. Identify the triangle and its angles

In this scenario, we have a triangle formed by Eid, the ball, and the goal. The known elements are:

• The distance from the ball to the goal: $b = 45 \text{ m}$
• The angle at the ball: $A = 45^\circ$
• The angle at Eid: $B = 35^\circ$

2. Calculate the remaining angle in the triangle

Using the triangle sum theorem, which states that the sum of the angles in a triangle equals $180^\circ$, we can find the angle at the goal:

$$ C = 180^\circ - A - B $$ Substituting the known values: $$ C = 180^\circ - 45^\circ - 35^\circ = 100^\circ $$

3. Apply the Law of Sines

Using the Law of Sines:

$$ \frac{a}{\sin A} = \frac{b}{\sin B} $$

Where:

• $a$ is the distance from Eid to the goal (what we want to find)
• $b = 45 \text{ m}$
• $A = 45^\circ$
• $B = 35^\circ$

Rearranging gives:

$$ a = b \cdot \frac{\sin A}{\sin B} $$

Substituting the values:

$$ a = 45 \cdot \frac{\sin 45^\circ}{\sin 35^\circ} $$

4. Calculate the sine values and final distance

Calculating the sine values:

• $\sin 45^\circ = \frac{\sqrt{2}}{2} \approx 0.7071$
• $\sin 35^\circ \approx 0.5736$

Now substituting these values into the equation:

$$ a \approx 45 \cdot \frac{0.7071}{0.5736} $$ $$ a \approx 45 \cdot 1.2337 \approx 55.51 \text{ m} $$