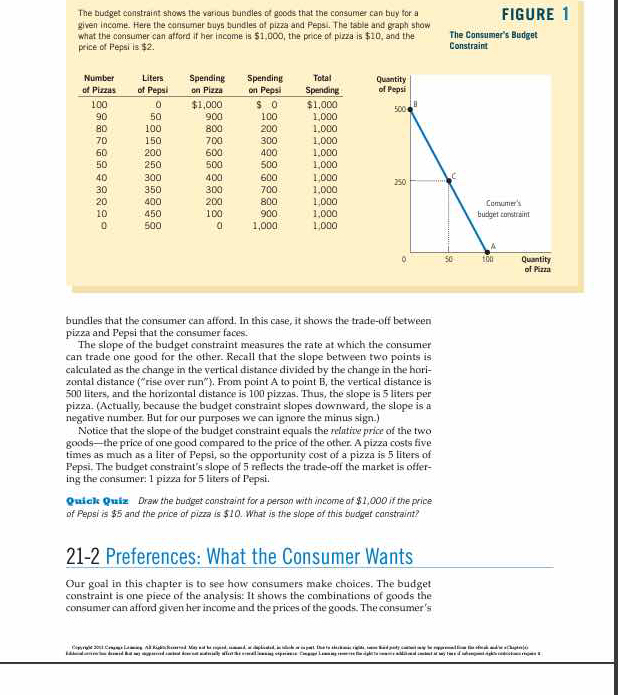
Draw the budget constraint for a person with income of $1,000 if the price of Pepsi is $5 and the price of pizza is $10. What is the slope of this budget constraint?
Understand the Problem
The question asks for the slope of the budget constraint given a consumer's income of $1,000, the price of pizza at $10, and the price of Pepsi at $5. This involves calculating the trade-off rate between the two goods, specifically how many liters of Pepsi can be obtained for one more pizza.
Answer
The slope of the budget constraint is \( -2 \).
Answer for screen readers
The slope of the budget constraint is ( -2 ).
Steps to Solve
- Identify the given values We have the following information:
- Income = $1,000
- Price of pizza = $10
- Price of Pepsi = $5
- Write the budget constraint equation
The budget equation is given by:
$$ I = P_p \cdot Q_p + P_P \cdot Q_P $$
Where:
- $I$ = Income
- $P_p$ = Price of pizza
- $Q_p$ = Quantity of pizza
- $P_P$ = Price of Pepsi
- $Q_P$ = Quantity of Pepsi
Substituting the given values:
$$ 1000 = 10 \cdot Q_p + 5 \cdot Q_P $$
- Find the slope of the budget constraint
The slope of the budget constraint represents the trade-off between pizza and Pepsi. This can be calculated as:
$$ \text{Slope} = -\frac{P_p}{P_P} $$
Substituting the known prices:
$$ \text{Slope} = -\frac{10}{5} = -2 $$
This means for every pizza, the consumer gives up 2 liters of Pepsi.
The slope of the budget constraint is ( -2 ).
More Information
The slope of the budget constraint indicates how much of one good (Pepsi) must be given up to obtain an additional unit of another good (pizza). Here, the consumer sacrifices 2 liters of Pepsi for each additional pizza.
Tips
- Confusing the slope with the actual quantities of goods; remember the slope provides the ratio of trade-offs, not the amounts themselves.
- Forgetting to use the correct prices in the slope formula.
AI-generated content may contain errors. Please verify critical information