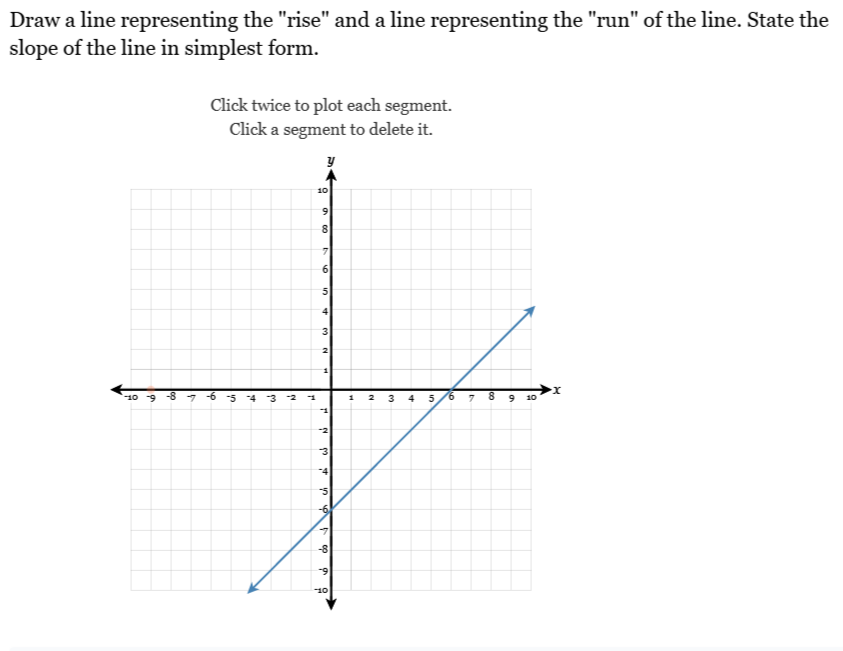
Draw a line representing the 'rise' and a line representing the 'run' of the line. State the slope of the line in simplest form.
Understand the Problem
The question is asking us to draw a line representing the 'rise' and another line representing the 'run' on a graph, and then to calculate the slope of the line in its simplest form. This involves recognizing the relationship between vertical change (rise) and horizontal change (run) and using those values to determine the slope.
Answer
The slope of the line is \( \frac{4}{3} \).
Answer for screen readers
The slope of the line is ( \frac{4}{3} ).
Steps to Solve
-
Identify Two Points on the Line
Choose two distinct points on the line for reference. For example, let’s say we pick points ( A(2, 3) ) and ( B(5, 7) ). -
Determine the Rise
The rise is the change in the ( y )-coordinates of the two points.
$$ \text{Rise} = y_2 - y_1 = 7 - 3 = 4 $$ -
Determine the Run
The run is the change in the ( x )-coordinates of the same points.
$$ \text{Run} = x_2 - x_1 = 5 - 2 = 3 $$ -
Calculate the Slope
The slope ( m ) of the line can be calculated using the formula:
$$ m = \frac{\text{Rise}}{\text{Run}} $$
Substituting the values we found:
$$ m = \frac{4}{3} $$ -
State the Slope in Simplest Form
The slope in simplest form is ( \frac{4}{3} ).
The slope of the line is ( \frac{4}{3} ).
More Information
The slope is a measure of how steep a line is, indicating the vertical change per unit of horizontal change. A positive slope like ( \frac{4}{3} ) means the line rises as it moves from left to right.
Tips
- Confusing rise and run. Make sure to correctly identify the vertical and horizontal changes.
- Not simplifying the slope to its simplest form. Check if the numerator and denominator can be reduced.
AI-generated content may contain errors. Please verify critical information