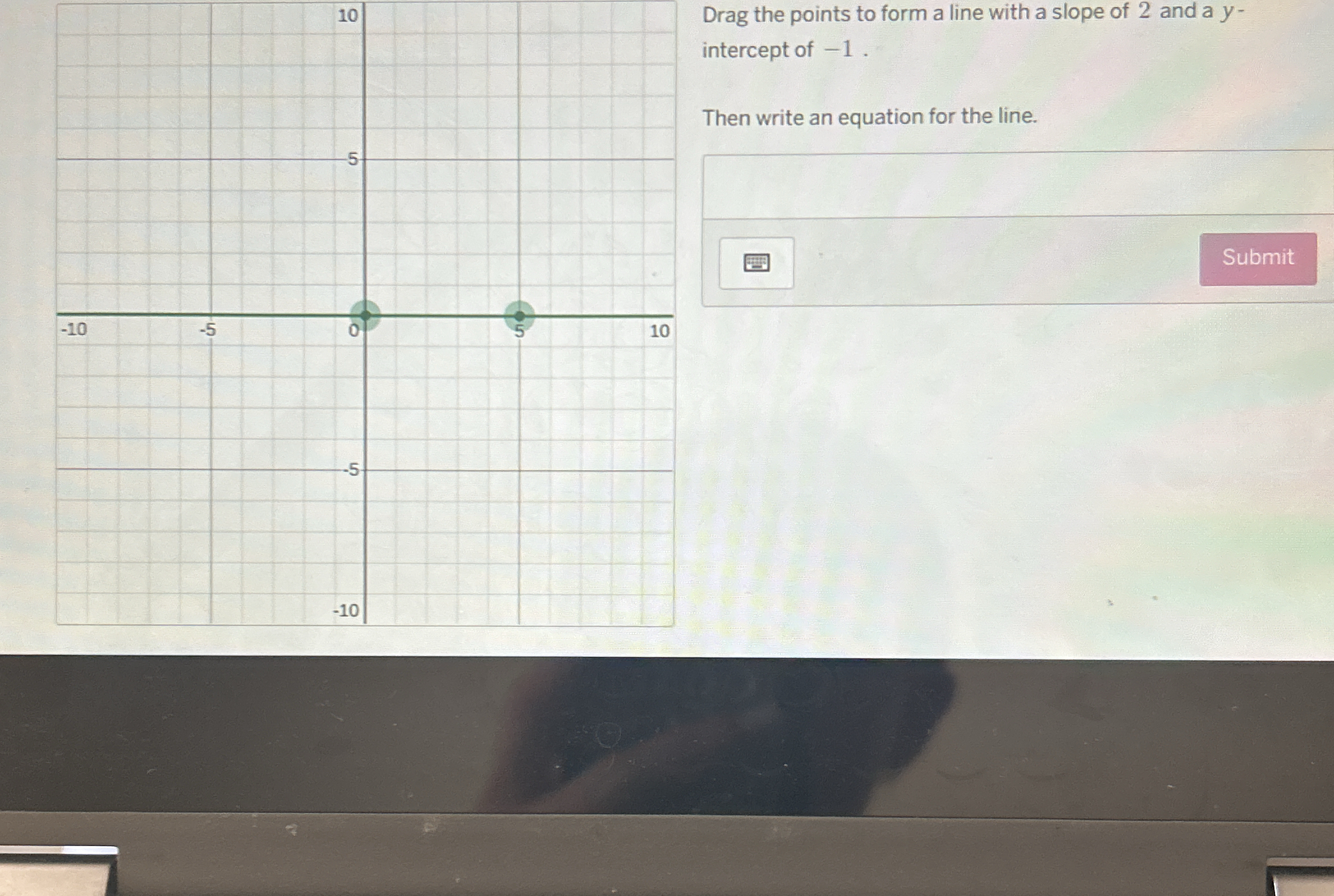
Drag the points to form a line with a slope of 2 and a y-intercept of -1. Then write an equation for the line.
Understand the Problem
The question asks to drag points to form a line with a specific slope and y-intercept, and then write the equation for that line. The slope given is 2 and the y-intercept is -1.
Answer
The equation of the line is \( y = 2x - 1 \).
Answer for screen readers
The equation of the line is ( y = 2x - 1 ).
Steps to Solve
-
Identify the y-intercept The y-intercept of the line is -1. This means that the line crosses the y-axis at the point (0, -1).
-
Identify the slope The slope given is 2. This indicates that for every 1 unit you move to the right (positive direction) along the x-axis, the line rises 2 units up along the y-axis.
-
Plot the first point Plot the first point at the y-intercept (0, -1) on the graph.
-
Use the slope to find the second point Starting from (0, -1), move 1 unit to the right to (1, -1), and then move up 2 units to (1, 1). This gives you your second point (1, 1).
-
Draw the line Connect the points (0, -1) and (1, 1) to form the line using the slope and y-intercept provided.
-
Write the equation of the line Now write the equation of the line in slope-intercept form, which is ( y = mx + b ), where ( m ) is the slope and ( b ) is the y-intercept. Thus, the equation is: $$ y = 2x - 1 $$
The equation of the line is ( y = 2x - 1 ).
More Information
The slope-intercept form of a linear equation is important as it makes graphing straightforward. The slope indicates the steepness of the line, while the y-intercept shows where the line crosses the y-axis.
Tips
- Forgetting to correctly interpret the slope; moving in the wrong direction.
- Mistaking the y-intercept point notation; ensuring it's (0, -1) and not just -1.
AI-generated content may contain errors. Please verify critical information