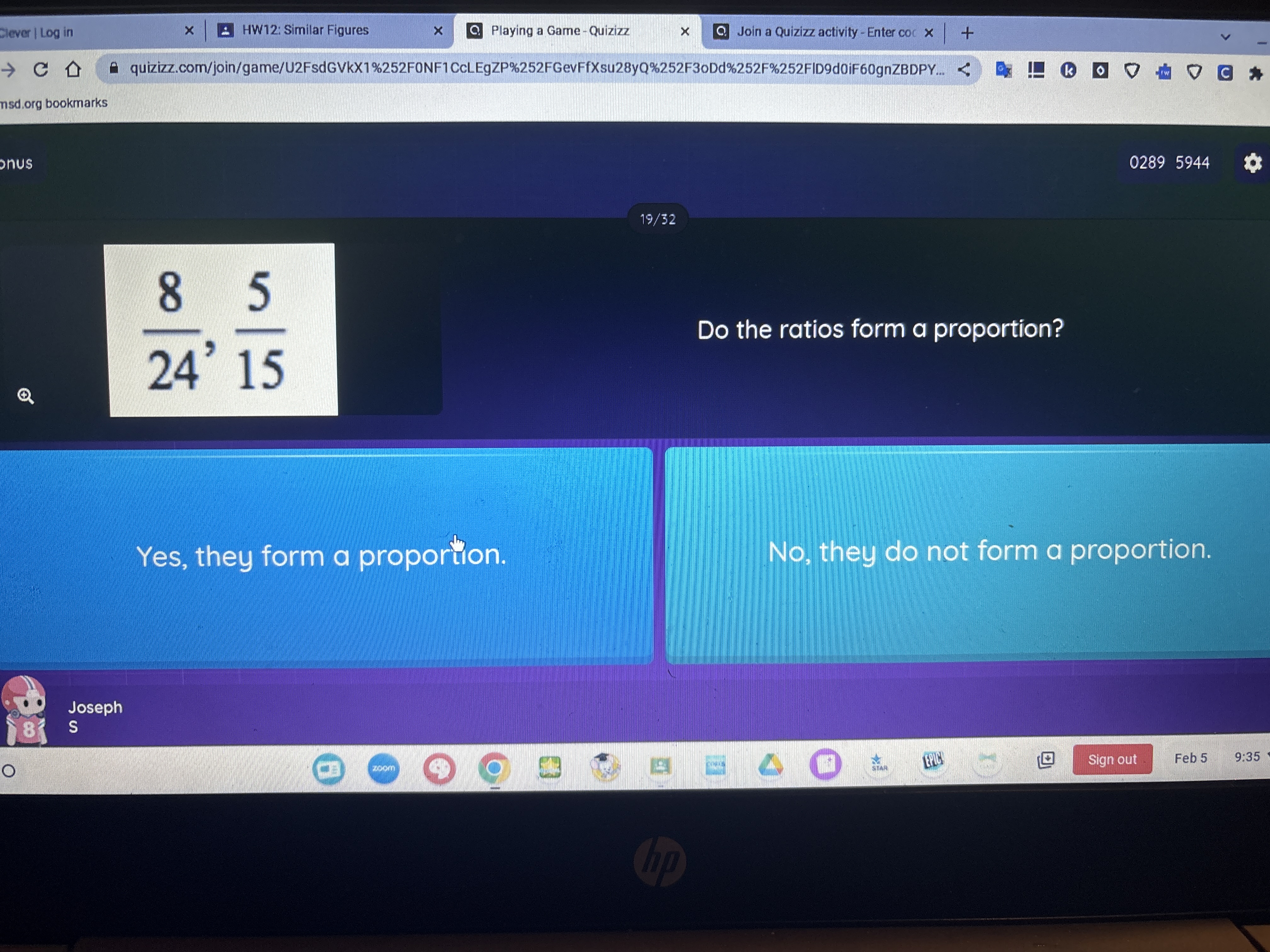
Do the ratios form a proportion?
Understand the Problem
The question is asking whether the given ratios form a proportion or not. To determine this, we can compare the cross-products of the ratios to see if they are equal.
Answer
Yes, the ratios \( \frac{8}{24} \) and \( \frac{5}{15} \) form a proportion.
Answer for screen readers
Yes, the ratios ( \frac{8}{24} ) and ( \frac{5}{15} ) form a proportion.
Steps to Solve
-
Set up the cross products To check if the ratios ( \frac{8}{24} ) and ( \frac{5}{15} ) form a proportion, we'll compare the cross products. This means we will calculate ( 8 \times 15 ) and ( 5 \times 24 ).
-
Calculate the first cross product Calculate ( 8 \times 15 ): [ 8 \times 15 = 120 ]
-
Calculate the second cross product Calculate ( 5 \times 24 ): [ 5 \times 24 = 120 ]
-
Compare the results Now we compare the two results: [ 120 \text{ (from the first product)} \quad \text{and} \quad 120 \text{ (from the second product)} ]
Since both cross products are equal, this indicates the ratios are proportional.
Yes, the ratios ( \frac{8}{24} ) and ( \frac{5}{15} ) form a proportion.
More Information
Proportions can be represented as fractions that are equivalent. In this case, both ratios simplify to ( \frac{1}{3} ), confirming they are proportional.
Tips
- Miscalculating Cross Products: Make sure to multiply correctly. Double-check your math to avoid errors.
- Not Simplifying Ratios First: Sometimes it's easier to simplify ratios before working with them; however, it's not necessary when you're comparing cross products directly.
AI-generated content may contain errors. Please verify critical information