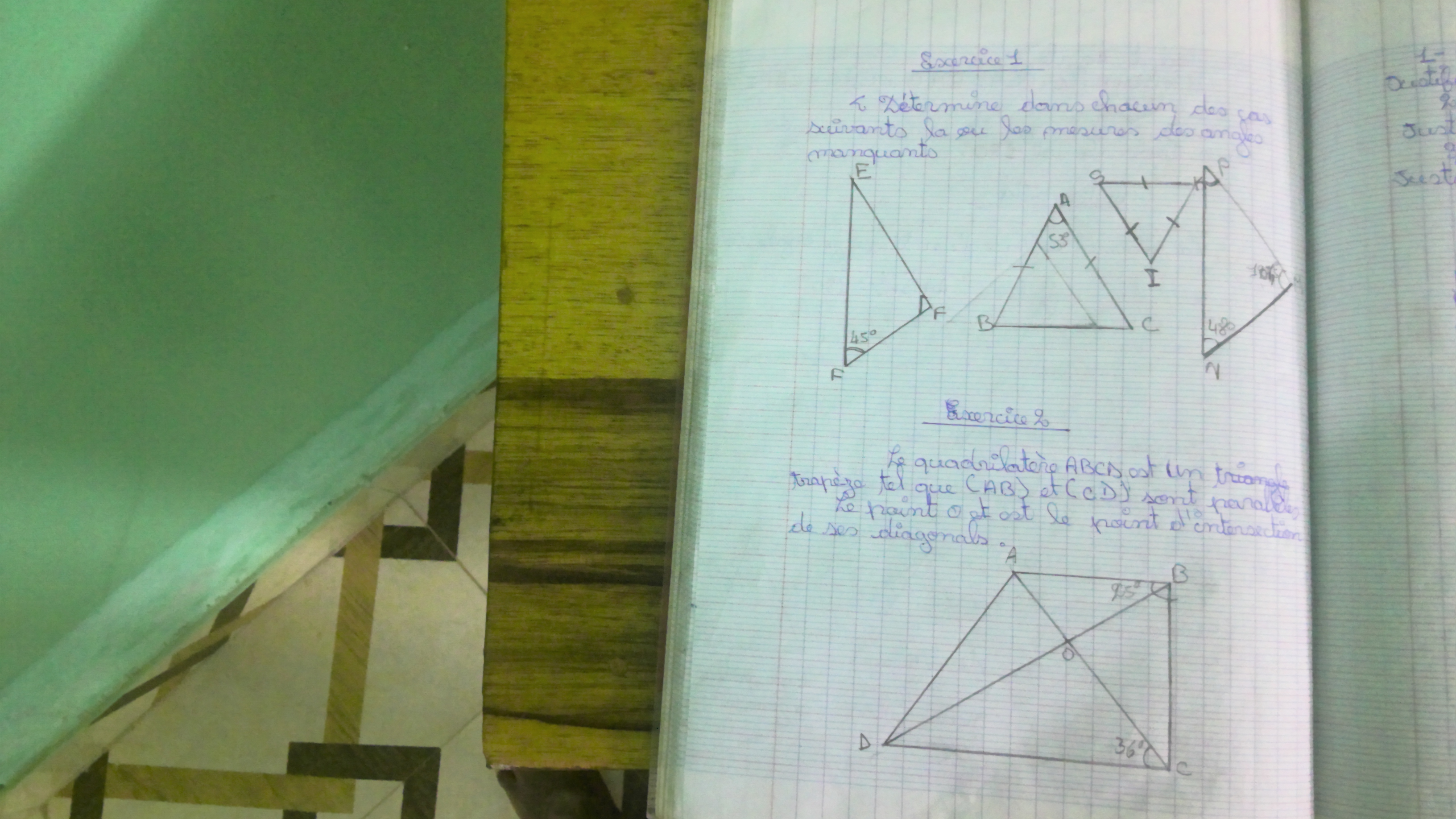
Déterminez dans chacun des cas suivants les mesures des angles manquants.
Understand the Problem
La question demande de déterminer les mesures des angles dans les figures géométriques présentées. Cela impliquera l'application de théorèmes de géométrie pour résoudre les triangles et les quadrilatères.
Answer
Les angles manquants sont F : $37^\circ$, I : $42^\circ$, D : $37^\circ$.
Answer for screen readers
Les mesures des angles sont les suivantes :
- Angle F dans le triangle 1 : $37^\circ$
- Angle I dans le triangle 2 : $42^\circ$
- Angle D dans le quadrilatère ABCD : $37^\circ$
Steps to Solve
- Déterminer les angles dans le triangle 1
Pour le triangle représentant les sommets A, B et F, nous avons un angle de $53^\circ$ donné. En utilisant la propriété que la somme des angles dans un triangle est $180^\circ$, nous pouvons calculer l'angle F:
$$ \text{Angle F} = 180^\circ - 53^\circ - 90^\circ = 37^\circ $$
- Déterminer les angles dans le triangle 2
Pour le triangle représentant les sommets C, I et A avec un angle de $48^\circ$, nous avons également un angle de $90^\circ$ (c'est un angle droit). Calculons l'angle I:
$$ \text{Angle I} = 180^\circ - 48^\circ - 90^\circ = 42^\circ $$
- Analyser le quadrilatère ABCD
Dans le quadrilatère ABCD, on nous dit que les lignes AB et CD sont parallèles. Nous avons des angles de $97^\circ$ et $36^\circ$ donnés. Pour trouver l’angle D, nous utilisons que la somme des angles dans un quadrilatère est $360^\circ$:
$$ \text{Angle D} = 360^\circ - (97^\circ + 36^\circ + 90^\circ) = 37^\circ $$
- Conclure sur les mesures des angles manquants
Nous avons maintenant tous les angles :
- Triangle 1 : $F = 37^\circ$
- Triangle 2 : $I = 42^\circ$
- Quadrilatère : $D = 37^\circ$
Les mesures des angles sont les suivantes :
- Angle F dans le triangle 1 : $37^\circ$
- Angle I dans le triangle 2 : $42^\circ$
- Angle D dans le quadrilatère ABCD : $37^\circ$
More Information
Ces calculs utilisent des propriétés géométriques fondamentales, notamment la somme des angles dans un triangle et un quadrilatère. Être capable de manipuler ces propriétés est essentiel pour résoudre des problèmes géométriques.
Tips
- Oublier que la somme des angles dans un triangle est $180^\circ$.
- Ne pas se rappeler que la somme des angles dans un quadrilatère est $360^\circ$.
- Confondre les angles adjacents dans les quadrilatères parallèles.
AI-generated content may contain errors. Please verify critical information