Determine whether the differential equation dR/dt + t cos R = e^{-t} is linear.
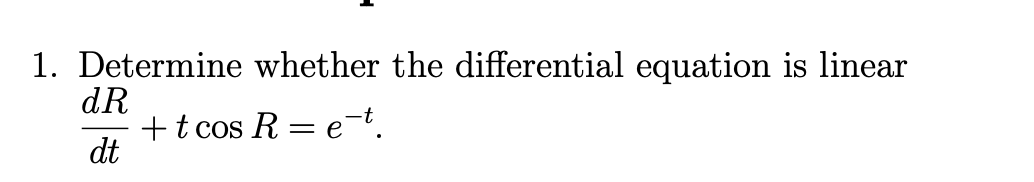
Understand the Problem
The question is asking to determine whether the given differential equation is linear or not. A linear differential equation has a specific structure, and we need to analyze the form of the equation provided.
Answer
The differential equation is not linear.
Answer for screen readers
The given differential equation is not linear.
Steps to Solve
- Identify the Form of the Differential Equation
A linear differential equation can be expressed in the form: $$ a(t) \frac{dR}{dt} + b(t) R = g(t) $$ where ( a(t) ), ( b(t) ), and ( g(t) ) are functions of ( t ) only, and ( R ) appears to the first power.
- Examine the Given Equation
The given differential equation is: $$ \frac{dR}{dt} + t \cos R = e^{-t} $$ Here, we have:
- ( \frac{dR}{dt} ) is the first derivative of ( R ),
- ( t \cos R ) is a term involving ( R ).
- Check the Non-Linearity Indicator
For the equation to be linear, ( R ) must only appear to the first power and not be multiplied by any function of ( R ) (e.g., ( \cos R )). The presence of ( \cos R ) indicates non-linearity.
- Conclusion
Since ( t \cos R ) includes a function of ( R ) (specifically, ( \cos R )), the differential equation is not linear.
The given differential equation is not linear.
More Information
Linear differential equations allow only functions of the independent variable (in this case, ( t )) to multiply or interact with the dependent variable (here, ( R )). However, since ( R ) is in a nonlinear function ( ( \cos R )), the equation does not meet the criteria for linearity.
Tips
- Confusing the presence of functions like sine or cosine of the dependent variable as linear. These terms indicate non-linearity.
- Not recognizing the requirement for dependent variables to be in first power only.
AI-generated content may contain errors. Please verify critical information