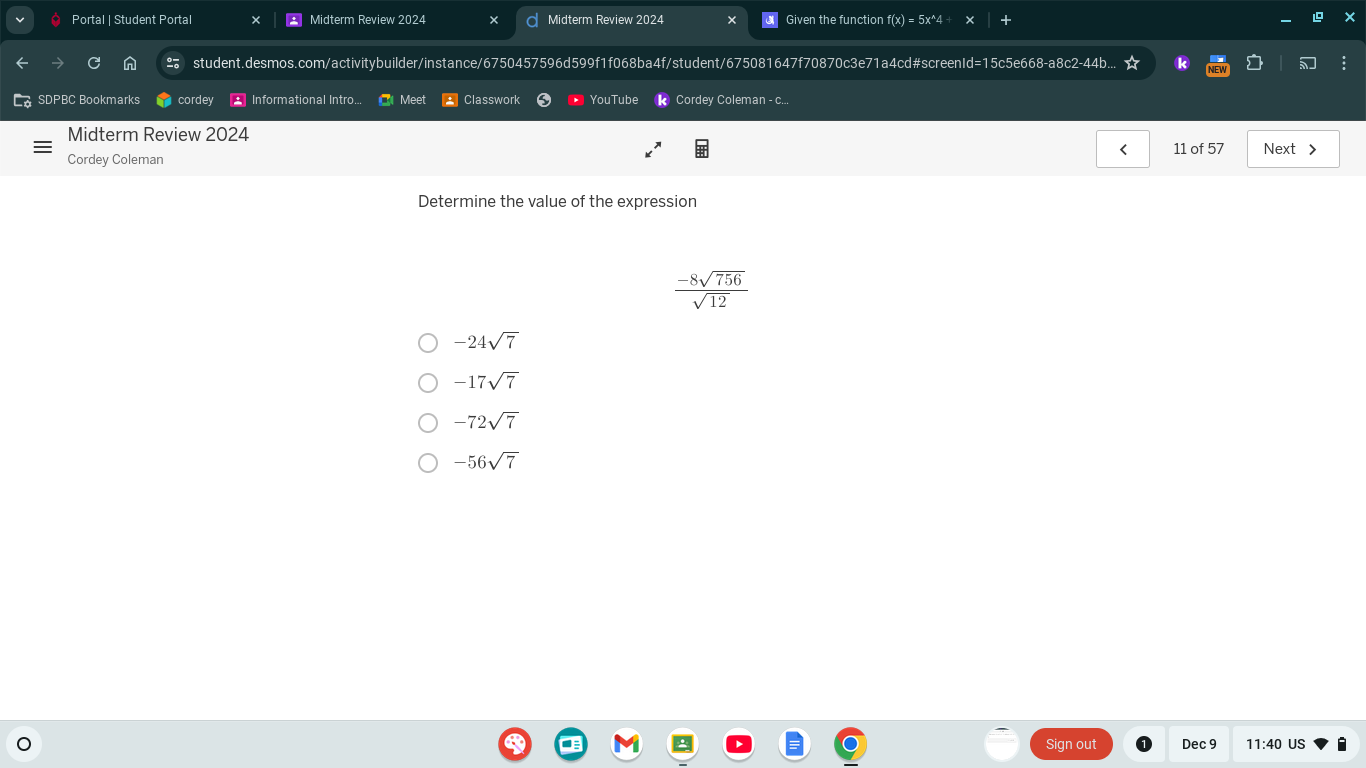
Determine the value of the expression -8√756/√12.

Steps to Solve

1. Simplify the Square Roots in the Expression

   Start with the expression: $$ -\frac{8\sqrt{756}}{\sqrt{12}} $$

   We can simplify the square roots separately. Begin with $\sqrt{756}$ and $\sqrt{12}$.

2. Factor the Numbers Under the Square Roots

   For $\sqrt{756}$: $$ 756 = 4 \times 189 = 4 \times 9 \times 21 = 36 \times 21 $$

   So, $$ \sqrt{756} = \sqrt{36 \times 21} = \sqrt{36} \times \sqrt{21} = 6\sqrt{21} $$

   For $\sqrt{12}$: $$ 12 = 4 \times 3 $$

   Thus, $$ \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} $$

3. Substitute the Simplified Square Roots Back into the Expression

   Now substitute the results into the original expression: $$ -\frac{8(6\sqrt{21})}{2\sqrt{3}} $$

   This simplifies to: $$ -\frac{48\sqrt{21}}{2\sqrt{3}} $$

4. Simplify the Fraction

   Dividing 48 by 2 gives: $$ -24 \frac{\sqrt{21}}{\sqrt{3}} $$

   Next, we simplify $\frac{\sqrt{21}}{\sqrt{3}}$: $$ \frac{\sqrt{21}}{\sqrt{3}} = \sqrt{\frac{21}{3}} = \sqrt{7} $$

5. Final Simplification

   Substitute this back into our expression: $$ -24 \sqrt{7} $$