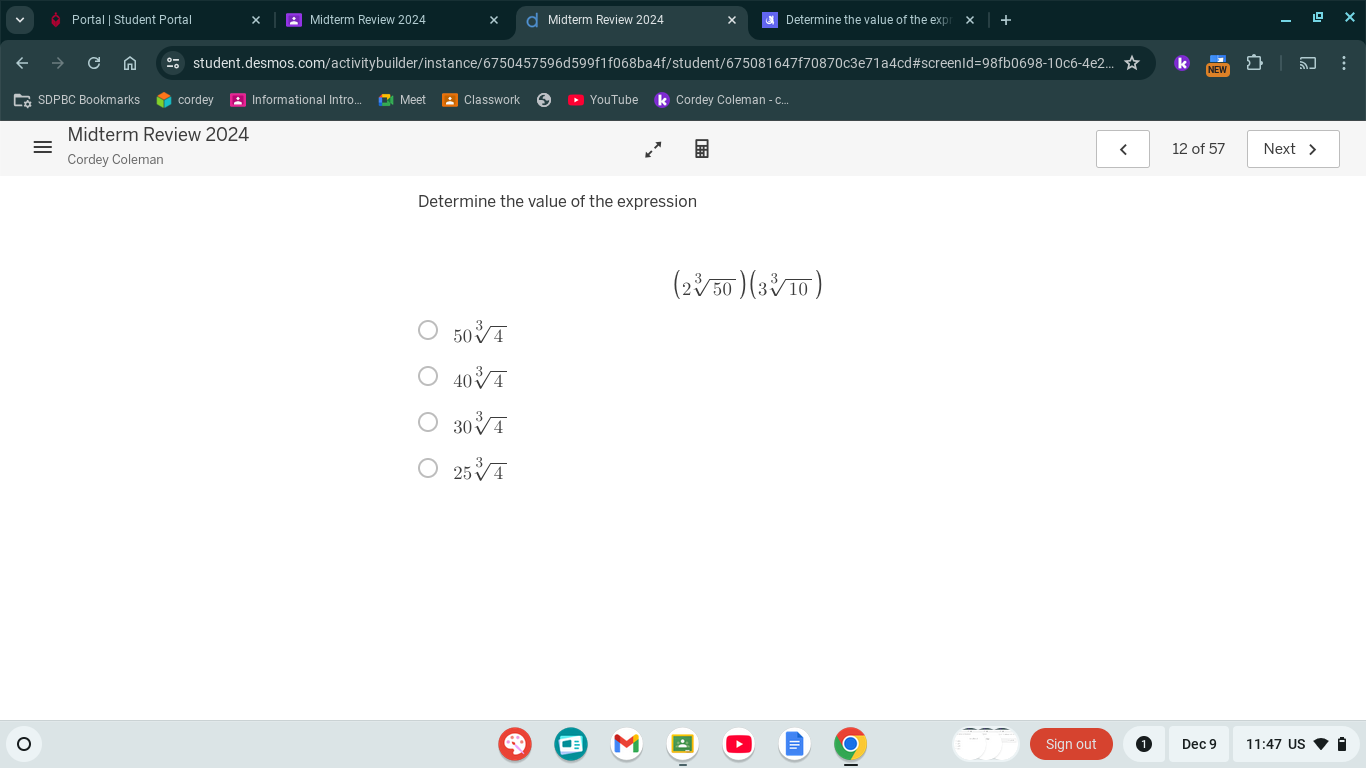
Determine the value of the expression (2^3√50)(3^3√10)
Understand the Problem
The question is asking to determine the value of the expression \((2^3\sqrt{50})(3^3\sqrt{10})\$. This involves simplifying the expression step by step to find the final result.
Answer
The final answer is \( 2160\sqrt{5} \).
Answer for screen readers
The value of the expression is ( 2160\sqrt{5} ).
Steps to Solve
-
Calculate Powers of Bases First, we calculate the powers: [ 2^3 = 8 \quad \text{and} \quad 3^3 = 27 ] Now we rewrite the expression: [ (2^3\sqrt{50})(3^3\sqrt{10}) = (8\sqrt{50})(27\sqrt{10}) ]
-
Multiply Constants Next, multiply the constants together: [ 8 \times 27 = 216 ] So we have: [ 216 (\sqrt{50}\sqrt{10}) ]
-
Combine Square Roots We combine the square roots: [ \sqrt{50} \times \sqrt{10} = \sqrt{500} ] Now the expression becomes: [ 216 \sqrt{500} ]
-
Simplify the Square Root Next, we simplify (\sqrt{500}): [ 500 = 100 \times 5 = 10^2 \times 5 ] Thus, [ \sqrt{500} = \sqrt{100 \times 5} = \sqrt{100} \times \sqrt{5} = 10\sqrt{5} ] So we have: [ 216 \sqrt{500} = 216 \times 10\sqrt{5} = 2160\sqrt{5} ]
-
Finalize the Expression Now we finalize the expression: [ 2160\sqrt{5} ]
The value of the expression is ( 2160\sqrt{5} ).
More Information
The expression involves powers and square roots, showcasing how to manipulate these mathematical elements to arrive at the final form. Simplifying square roots and multiplying constants are key skills used here.
Tips
Common mistakes include:
- Not simplifying square roots correctly, especially miscalculating factors.
- Forgetting to multiply all parts of the expression together.
- Ignoring the properties of exponents during simplification.
AI-generated content may contain errors. Please verify critical information