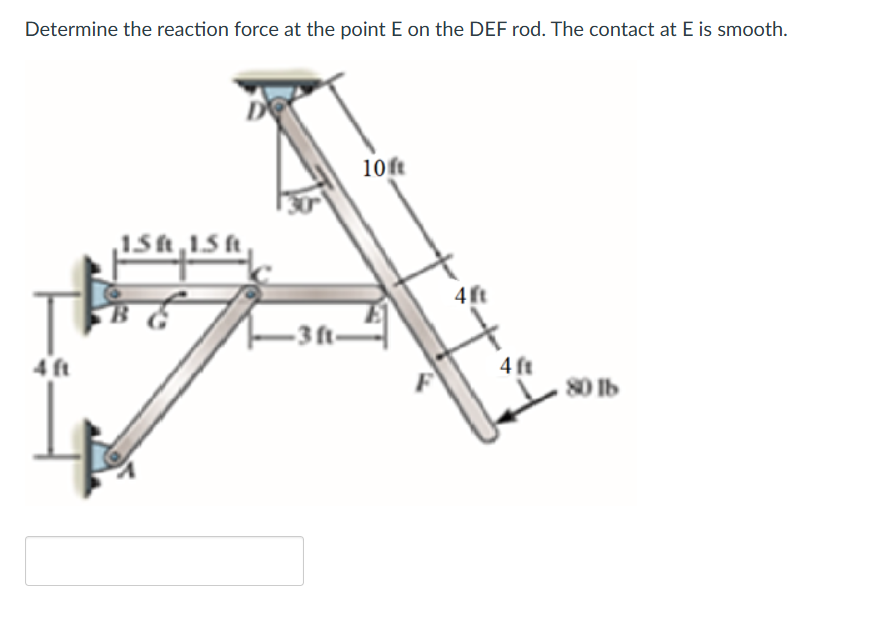
Determine the reaction force at the point E on the DEF rod. The contact at E is smooth.

Steps to Solve

1. Identify the Forces Acting on the System

The forces acting are:

• The weight force at point F (80 lb down).
• The reaction force at point E, which we need to determine.
• The vertical reactions at points A and B.

2. Determine Moment about Point E

To find the reaction force at E, apply the moment equation around point E.

Use the equation: $$ \sum M_E = 0 $$

The moment due to the 80 lb force needs to be calculated. The distance from E to F is 4 ft, and from E to D is the vertical component of the position determined by the angle (30 degrees). Since $D$ is directly over $E$, its arm is just $10\text{ ft}$.

The moment equation becomes: $$ 80 \text{ lb} \times 4 \text{ ft} - R_E \times 10 \text{ ft} = 0 $$ where $R_E$ is the reaction force at point E.

3. Solve for Reaction Force at Point E

Rearranging the equation to find $R_E$, we have: $$ R_E = \frac{80 \text{ lb} \times 4 \text{ ft}}{10 \text{ ft}} $$

Now calculate: $$ R_E = \frac{320 \text{ lb ft}}{10 \text{ ft}} = 32 \text{ lb} $$

4. Check if Forces are in Equilibrium

To ensure that the system is in equilibrium, verify that the sum of vertical forces is equal to zero. The vertical reactions at points A and B must support the weight acting downward. Calculate if these reactions balance out with gravity and the derived force at E.