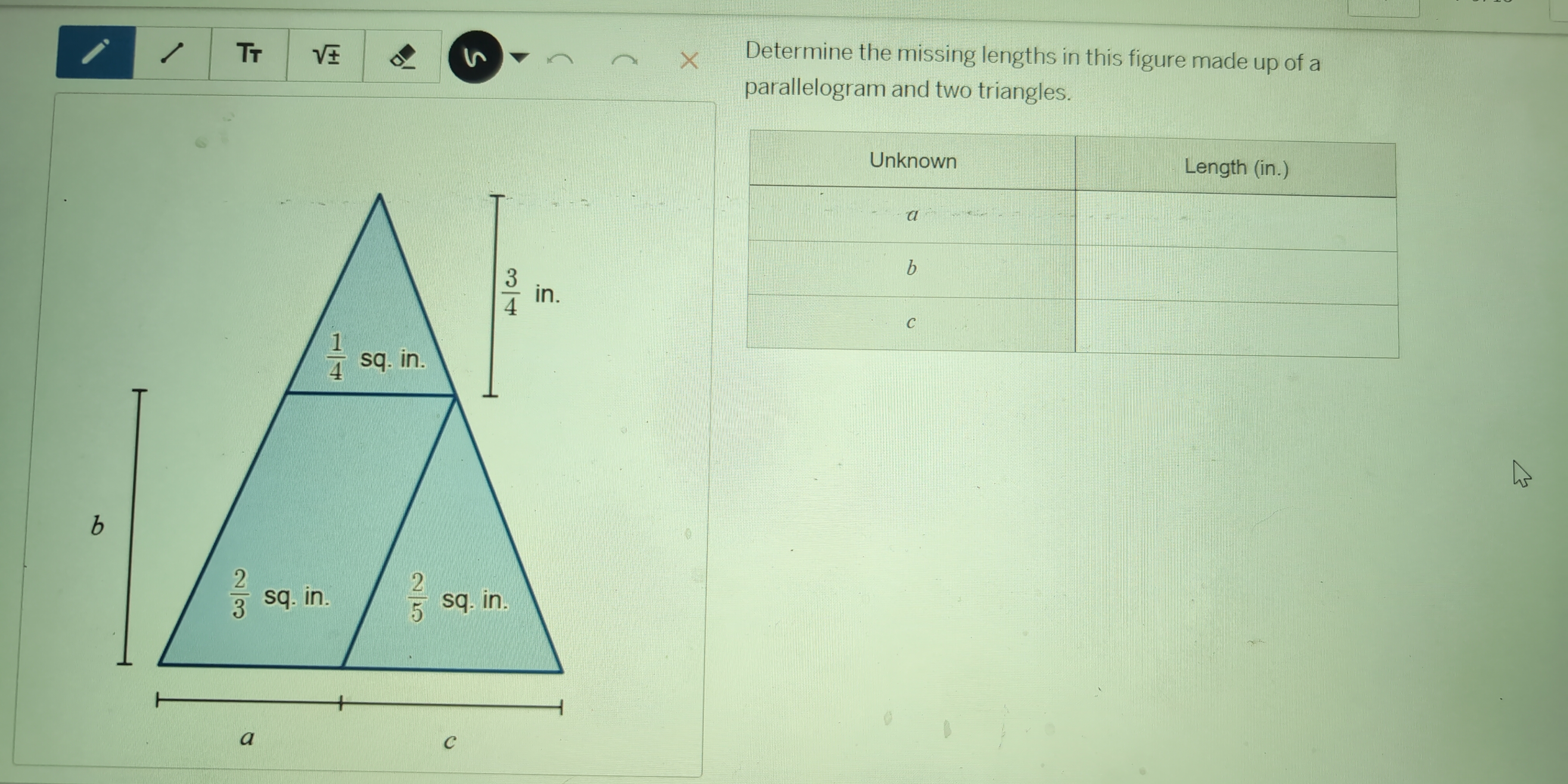
Determine the missing lengths in this figure made up of a parallelogram and two triangles.

Steps to Solve

1. Identify the areas of triangles

   The area of a triangle can be expressed as: $$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $$

   We'll use this formula to calculate the lengths of unknowns ( a, b, ) and ( c ).

2. Calculate ( b ) using triangle with area ( \frac{1}{4} ) sq. in.

   The height of this triangle is given as ( \frac{3}{4} ) in.

   Set up the equation: $$ \frac{1}{4} = \frac{1}{2} \times a \times \frac{3}{4} $$

   Solving for ( a ): $$ \frac{1}{4} = \frac{3a}{8} $$ Multiply both sides by 8: $$ 2 = 3a $$ $$ a = \frac{2}{3} \text{ in.} $$

3. Calculate ( b ) using triangle with area ( \frac{2}{3} ) sq. in.

   The base of this triangle is ( c ) and let ( b ) be the height.

   Set up the equation: $$ \frac{2}{3} = \frac{1}{2} \times c \times b $$

   Solving for ( b ): $$ \frac{2}{3} = \frac{cb}{2} $$ Multiply both sides by 2: $$ \frac{4}{3} = cb $$ Rearranging gives: $$ b = \frac{4}{3c} $$

4. Calculate ( c ) using triangle with area ( \frac{2}{5} ) sq. in.

   The height is ( b ) and the base is ( a ).

   Set up the equation: $$ \frac{2}{5} = \frac{1}{2} \times a \times b $$

   Solving for ( c ): Substitute ( a = \frac{2}{3} ): $$ \frac{2}{5} = \frac{1}{2} \times \frac{2}{3} \times b $$ $$ \frac{2}{5} = \frac{b}{3} $$ Multiply by 3: $$ \frac{6}{5} = b $$

   Now use ( b ) in the equation for ( c ): $$ b = \frac{4}{3c} $$ Substitute ( b = \frac{6}{5} ): $$ \frac{6}{5} = \frac{4}{3c} $$ Cross-multiply and solve: $$ 6 \times 3c = 4 \times 5 $$ $$ 18c = 20 $$ $$ c = \frac{20}{18} = \frac{10}{9} \text{ in.} $$

5. List final values

   Now we have:

   • ( a = \frac{2}{3} \text{ in.} )
   • ( b = \frac{6}{5} \text{ in.} )
   • ( c = \frac{10}{9} \text{ in.} )