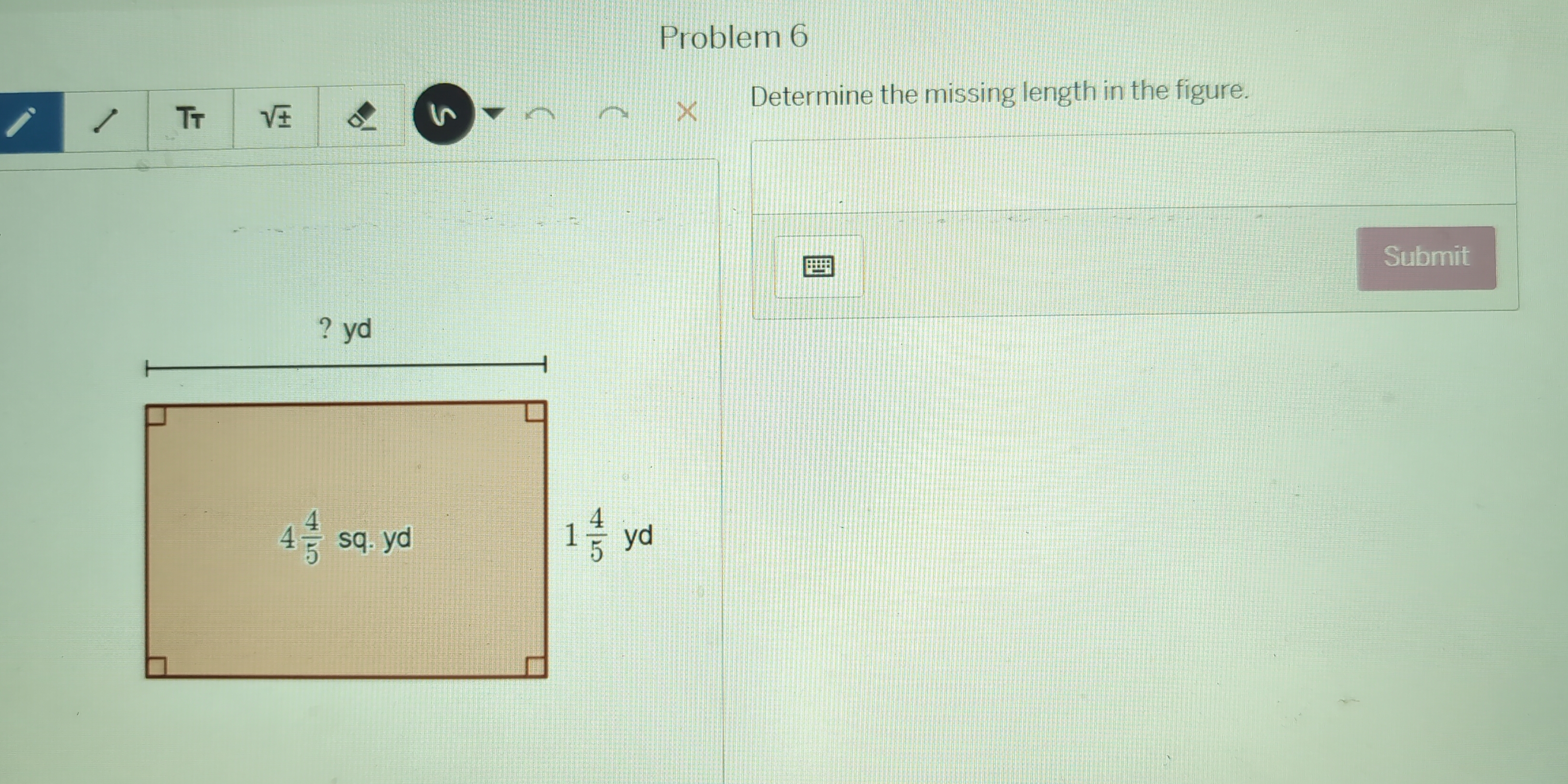
Determine the missing length in the figure.
Understand the Problem
The question is asking to determine a missing length of a rectangle given its area and one side length. The problem involves understanding the relationship between area, length, and width in geometrical figures.
Answer
The missing length is \( \frac{8}{3} \) yards or \( 2 \frac{2}{3} \) yards.
Answer for screen readers
The missing length is ( \frac{8}{3} ) yards, or ( 2 \frac{2}{3} ) yards.
Steps to Solve
-
Identify the Given Information The area of the rectangle is given as (4 \frac{4}{5}) square yards and one side length (width) is (1 \frac{4}{5}) yards.
-
Convert Mixed Numbers to Improper Fractions First, convert the mixed numbers to improper fractions for easier calculations.
For the area: [ 4 \frac{4}{5} = \frac{24}{5} \text{ square yards} ] For the width: [ 1 \frac{4}{5} = \frac{9}{5} \text{ yards} ]
-
Use the Area Formula The formula for the area of a rectangle is: $$ \text{Area} = \text{Length} \times \text{Width} $$ Substituting the known values: $$ \frac{24}{5} = \text{Length} \times \frac{9}{5} $$
-
Isolate the Length To find the length, divide both sides by (\frac{9}{5}): $$ \text{Length} = \frac{24}{5} \div \frac{9}{5} = \frac{24}{5} \times \frac{5}{9} $$
-
Simplify the Expression The fives in the numerator and denominator cancel out: $$ \text{Length} = \frac{24}{9} = \frac{8}{3} \text{ yards} $$
-
Convert to Mixed Number (if needed) To convert (\frac{8}{3}) to a mixed number: [ 8 \div 3 = 2 \text{ R } 2 \Rightarrow 2 \frac{2}{3} \text{ yards} ]
The missing length is ( \frac{8}{3} ) yards, or ( 2 \frac{2}{3} ) yards.
More Information
Finding the length of a rectangle involves using the formula for area, which connects length and width. This understanding is fundamental in geometry and helps in solving real-world problems related to space.
Tips
- Not converting mixed numbers correctly: Ensure you understand the conversion process from mixed numbers to improper fractions to avoid calculation errors.
- Confusing multiplication and division in area calculations: Remember that to isolate length, we divide by the width, not multiply.
AI-generated content may contain errors. Please verify critical information