Determine the domain, range, and discontinuities of the piecewise function g(x) given.

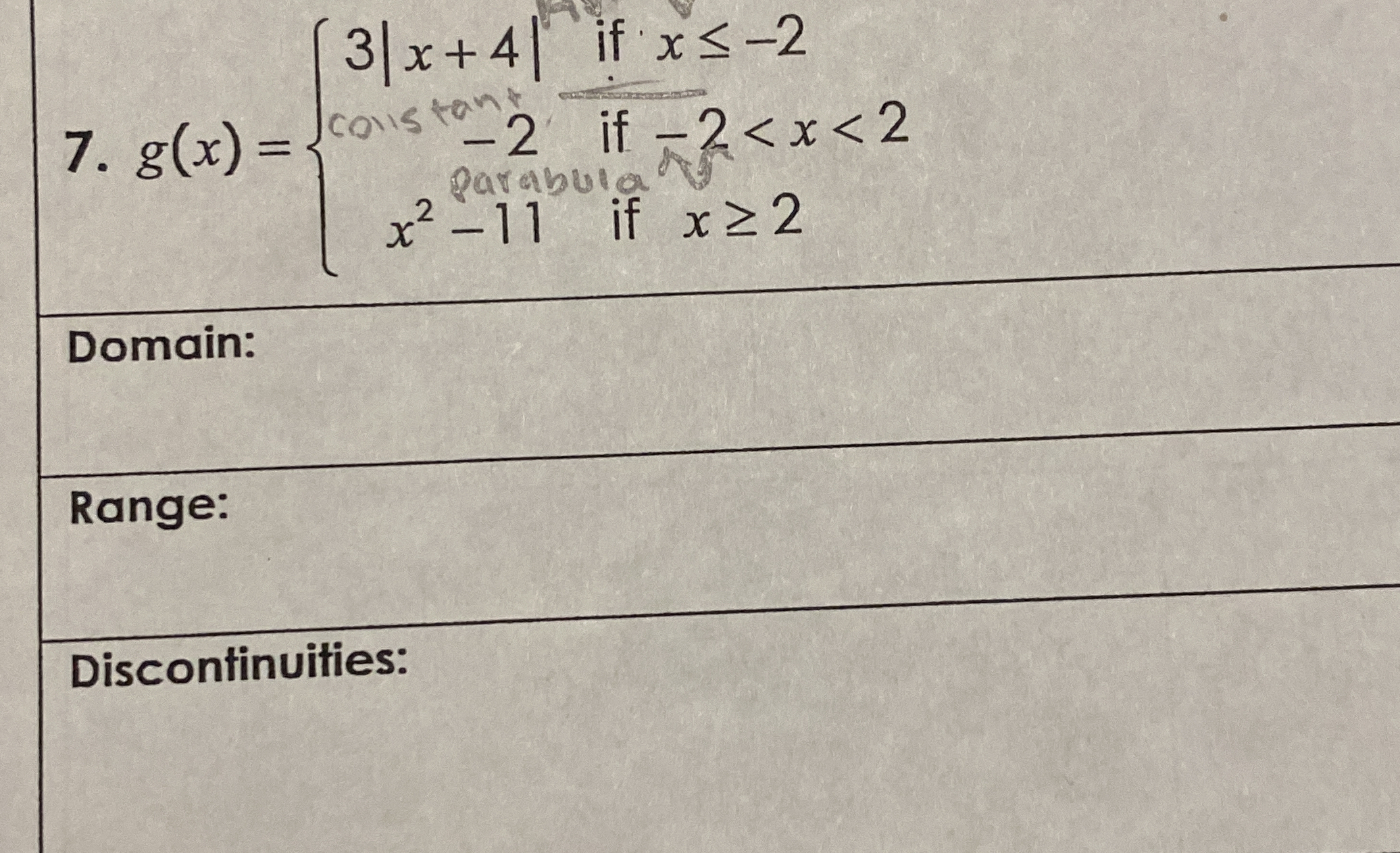
Understand the Problem

The question is asking to find the domain, range, and any discontinuities of the piecewise function g(x) given in the image. This requires analyzing each piece of the function and determining the valid x-values (domain), the corresponding y-values (range), and where the function may not be continuous.

Answer

Domain: $(-\infty, 2]$, Range: $[-7, 6]$, Discontinuities: $x = -2, 2$

Steps to Solve

Identify the Domain The function is defined in three segments:

For $x \leq -2$, $3|x + 4|$ is defined.
For $-2 < x < 2$, $-2$ is defined.
For $x \geq 2$, $x^2 - 11$ is defined.

Thus, the domain is all values of $x$ where the function is defined:
$$ \text{Domain: } (-\infty, 2] $$

Find the Range Next, evaluate the output values for each segment of the function:

For $x \leq -2$: Calculate the maximum value at $x = -2$: $$ g(-2) = 3|-2 + 4| = 3 \cdot 2 = 6 $$
As $x$ goes to $-\infty$, $g(x)$ also goes to $\infty$.
For $-2 < x < 2$: The value is constant at $-2$.
For $x \geq 2$: Find the values for this segment: $$ g(2) = 2^2 - 11 = 4 - 11 = -7 $$
As $x$ increases to $+\infty$, $g(x)$ approaches $+\infty$.

Combining these, we find the range:
$$ \text{Range: } [-7, 6] $$

Determine Discontinuities Check the points where the function changes its definition, especially at the boundaries $x = -2$ and $x = 2$:

At $x = -2$, we check:
- Left: $g(-2) = 6$
- Right: $g(-2) = -2$ (at the next piece)

This shows a jump discontinuity.

At $x = 2$, we check:
- Left: $g(2) = -2$
- Right: $g(2) = -7$

This also indicates a jump discontinuity.

Thus, the discontinuities are at:
$$ \text{Discontinuities: } x = -2, 2 $$

Domain: $(-\infty, 2]$
Range: $[-7, 6]$
Discontinuities: $x = -2, 2$

More Information

The function combines multiple types of equations, including an absolute value, a constant, and a quadratic, which creates interesting behavior. The analysis of the domain and range illustrates how piecewise functions can showcase discontinuities—where the output jumps from one value to another without taking on the 'in-between' values.

Tips

Forgetting to check the endpoints of the intervals can lead to missing values in the domain or range.
Miscalculating function values at the transition points hides discontinuities.
Not considering that a jump discontinuity occurs when the left-hand limit and right-hand limit do not match.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!