Determine the defined range for sin(x) + sin(x)cot(x)² = sec(x).
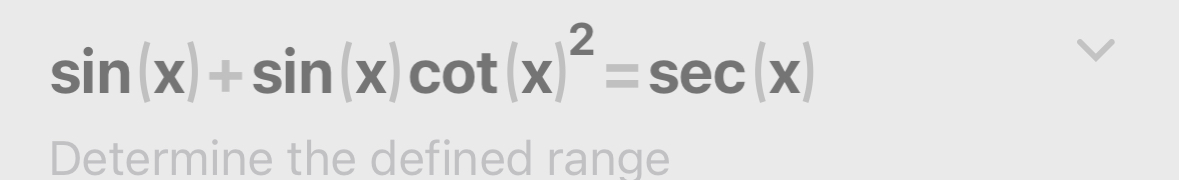
Understand the Problem
The question is asking to determine the defined range for the equation involving trigonometric functions: sin(x) + sin(x)cot(x)² = sec(x). This involves analyzing the functions to find valid input values for x that will satisfy the equation.
Answer
The defined range for $x$ varies based on the solution to the derived quadratic equation and the restrictions from $\sin(x)$ and $\cos(x)$. Typically, examine intervals within $x \in [0, \pi]$.
Answer for screen readers
The defined range for $x$ will be found by solving the quadratic equation obtained from the relationships above. The restrictions from $\sin(x)$ and $\cos(x)$ lead to valid input range typically between $[0, \pi]$ but further analysis may reveal specific valid intervals for solutions.
Steps to Solve
- Rewrite the equation with trigonometric identities
We start by rewriting $\cot(x)$ and $\sec(x)$ in terms of sine and cosine. We know: $$ \cot(x) = \frac{\cos(x)}{\sin(x)} $$ $$ \sec(x) = \frac{1}{\cos(x)} $$
- Substitute the identities into the equation
Substituting these identities into the original equation gives us: $$ \sin(x) + \sin(x) \left(\frac{\cos(x)}{\sin(x)}\right)^2 = \frac{1}{\cos(x)} $$
- Simplify the equation
The equation simplifies to: $$ \sin(x) + \sin(x) \frac{\cos^2(x)}{\sin^2(x)} = \frac{1}{\cos(x)} $$ $$ \sin(x) + \frac{\cos^2(x)}{\sin(x)} = \frac{1}{\cos(x)} $$
- Multiply through by $\sin(x)\cos(x)$ to eliminate denominators
To eliminate denominators, multiply the entire equation by $\sin(x)\cos(x)$: $$ \sin^2(x)\cos(x) + \cos^2(x) = \sin(x) $$
- Rearrange the equation
Rearranging terms gives us: $$ \sin^2(x)\cos(x) - \sin(x) + \cos^2(x) = 0 $$
- Factor or use the quadratic formula
Let $y = \sin(x)$: $$ y^2 \cos(x) - y + \cos^2(x) = 0 $$ This is a quadratic equation in $y$ which we can solve using the quadratic formula: $$ y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ Here, $a = \cos(x)$, $b = -1$, and $c = \cos^2(x)$.
- Determine valid values for x
This will lead to restrictions on $\sin(x)$ and $\cos(x)$, and by finding the range of values for $y$, you will be able to find the corresponding range for $x$.
The defined range for $x$ will be found by solving the quadratic equation obtained from the relationships above. The restrictions from $\sin(x)$ and $\cos(x)$ lead to valid input range typically between $[0, \pi]$ but further analysis may reveal specific valid intervals for solutions.
More Information
The functions involved are periodic, and examining each interval gives insight into the solutions that satisfy the equation. This approach shows how to analyze trigonometric equations effectively.
Tips
- Neglecting to check for division by zero in trigonometric functions (like when $cos(x) = 0$).
- Forgetting to apply periodic properties of trigonometric functions when determining the range.
- Misapplying the quadratic formula or not considering both roots of the equation.
AI-generated content may contain errors. Please verify critical information