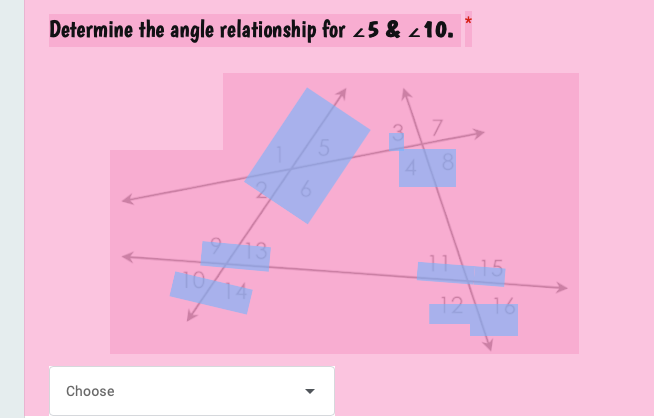
Determine the angle relationship for ∠5 & ∠10.
Understand the Problem
The question is asking us to determine the angle relationship between angles 5 and 10, which likely involves identifying whether they are corresponding, alternate interior, or some other type of angle relationship based on the intersecting lines shown.
Answer
The angle relationship between ∠5 and ∠10 is that they are alternate exterior angles.
Answer for screen readers
The angle relationship between ∠5 and ∠10 is that they are alternate exterior angles.
Steps to Solve
-
Identify the angles
We identify that angle 5 is located on one transversal and angle 10 is on the opposite transversal. -
Determine angle types
Angle 5 and angle 10 are formed by the intersection of a pair of parallel lines and two transversals, which helps in categorizing them. -
Classify the relationship
Since both angles are located on opposite sides of the transversal and above the parallel lines, they are classified as alternate exterior angles. -
Conclusion on angle relationship
Based on the classification, we can conclude that angle 5 and angle 10 are equal due to the properties of alternate exterior angles formed by parallel lines.
The angle relationship between ∠5 and ∠10 is that they are alternate exterior angles.
More Information
Alternate exterior angles are formed when two parallel lines are cut by a transversal, and they are equal in measure. This property is useful in geometry for solving various problems involving angle relationships.
Tips
- Confusing alternate interior with exterior angles: It’s essential to correctly identify the positions of the angles relative to the parallel lines and transversal.
- Assuming angles are not equal: Remember that alternate exterior angles are always equal when formed by parallel lines.
AI-generated content may contain errors. Please verify critical information