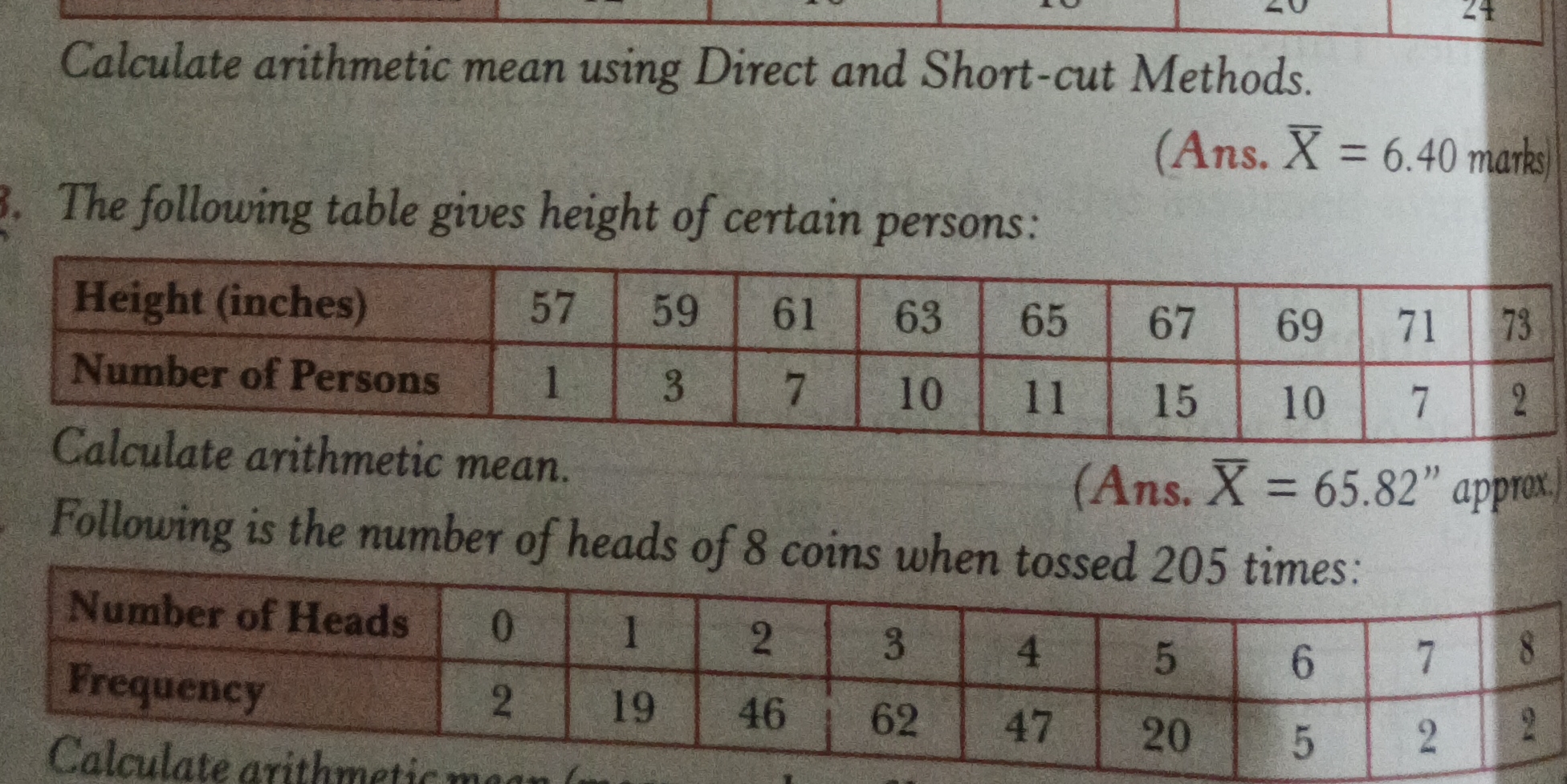
Calculate the arithmetic mean for the following questions: 1. Calculate arithmetic mean using Direct and Short-cut Methods. 2. The following table gives height of certain persons... Calculate the arithmetic mean for the following questions: 1. Calculate arithmetic mean using Direct and Short-cut Methods. 2. The following table gives height of certain persons, calculate the arithmetic mean: Height (inches): 57, 59, 61, 63, 65, 67, 69, 71, 73; Number of Persons: 1, 3, 7, 10, 11, 15, 10, 7, 2. 3. Following is the number of heads of 8 coins when tossed 205 times, calculate the arithmetic mean: Number of Heads: 0, 1, 2, 3, 4, 5, 6, 7, 8; Frequency: 2, 19, 46, 62, 47, 20, 5, 2, 2. Read more

Steps to Solve

1. Calculate the arithmetic mean using the direct method for the first table

The direct method formula for arithmetic mean is:

$\overline{X} = \frac{\sum f_i x_i}{\sum f_i}$

Where $x_i$ are the heights and $f_i$ are the corresponding frequencies (number of persons).

$ \sum f_i x_i = (57 \times 1) + (59 \times 3) + (61 \times 7) + (63 \times 10) + (65 \times 11) + (67 \times 15) + (69 \times 10) + (71 \times 7) + (73 \times 2) = 57 + 177 + 427 + 630 + 715 + 1005 + 690 + 497 + 146 = 4344 $

$ \sum f_i = 1 + 3 + 7 + 10 + 11 + 15 + 10 + 7 + 2 = 66 $

Therefore, the arithmetic mean is:

$ \overline{X} = \frac{4344}{66} = 65.8181... \approx 65.82 $

2. Calculate the arithmetic mean using the short-cut method for the first table

The short-cut method formula for arithmetic mean is:

$\overline{X} = A + \frac{\sum f_i d_i}{\sum f_i}$

Where $A$ is the assumed mean, $d_i = x_i - A$ is the deviation from the assumed mean, and $f_i$ are the corresponding frequencies. Let's assume the mean $A = 65$.

Now we need to calculate $d_i$ for each $x_i$:

$d_1 = 57 - 65 = -8$ $d_2 = 59 - 65 = -6$ $d_3 = 61 - 65 = -4$ $d_4 = 63 - 65 = -2$ $d_5 = 65 - 65 = 0$ $d_6 = 67 - 65 = 2$ $d_7 = 69 - 65 = 4$ $d_8 = 71 - 65 = 6$ $d_9 = 73 - 65 = 8$

Now we need to calculate $f_i \times d_i$ for each $i$:

$f_1 d_1 = 1 \times -8 = -8$ $f_2 d_2 = 3 \times -6 = -18$ $f_3 d_3 = 7 \times -4 = -28$ $f_4 d_4 = 10 \times -2 = -20$ $f_5 d_5 = 11 \times 0 = 0$ $f_6 d_6 = 15 \times 2 = 30$ $f_7 d_7 = 10 \times 4 = 40$ $f_8 d_8 = 7 \times 6 = 42$ $f_9 d_9 = 2 \times 8 = 16$

$ \sum f_i d_i = -8 -18 -28 -20 + 0 + 30 + 40 + 42 + 16 = 54 $ $ \sum f_i = 66 $

Therefore, the arithmetic mean is:

$ \overline{X} = 65 + \frac{54}{66} = 65 + 0.8181... = 65.8181... \approx 65.82 $

3. Calculate the arithmetic mean for the second table

The direct method formula for arithmetic mean is:

$\overline{X} = \frac{\sum f_i x_i}{\sum f_i}$

Where $x_i$ are the number of heads and $f_i$ are the corresponding frequencies.

$ \sum f_i x_i = (0 \times 2) + (1 \times 19) + (2 \times 46) + (3 \times 62) + (4 \times 47) + (5 \times 20) + (6 \times 5) + (7 \times 2) + (8 \times 2) = 0 + 19 + 92 + 186 + 188 + 100 + 30 + 14 + 16 = 645 $ $ \sum f_i = 2 + 19 + 46 + 62 + 47 + 20 + 5 + 2 + 2 = 205 $

Therefore, the arithmetic mean is:

$ \overline{X} = \frac{677}{205} = 3.3 $