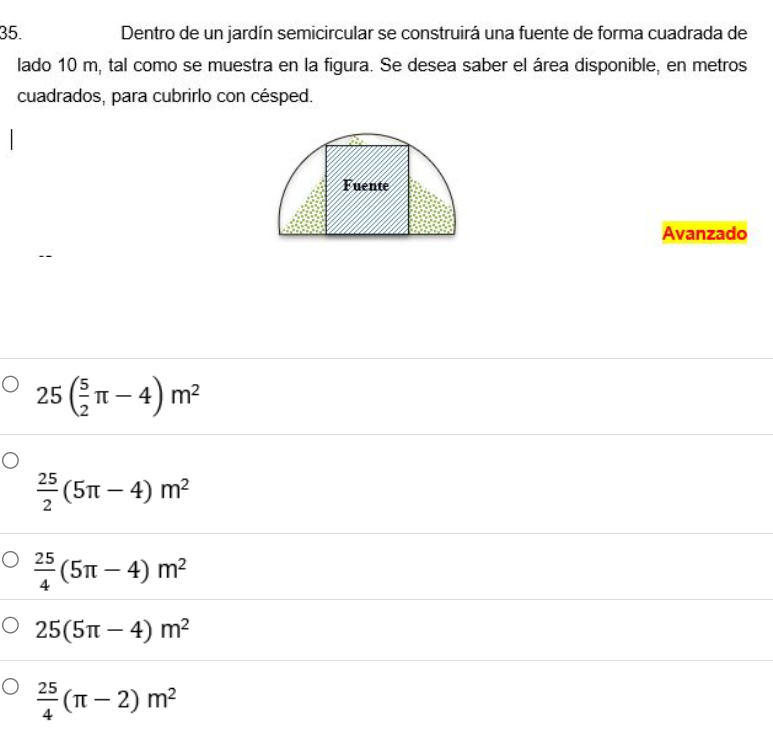
Dentro de un jardín semicircular se construirá una fuente de forma cuadrada de lado 10 m. Se desea saber el área disponible, en metros cuadrados, para cubrirlo con césped.

Understand the Problem

La pregunta está pidiendo calcular el área disponible en un jardín semicircular que tiene una fuente cuadrada en su interior. Se requiere encontrar el área que queda disponible para cubrir con césped, en metros cuadrados.

Answer

El área disponible para cubrir con césped es $ 25(2\pi - 4) \, m^2 $.

Steps to Solve

Calcular el área del jardín semicircular

El área de un círculo se calcula con la fórmula ( A = \pi r^2 ). Dado que el jardín es semicircular y tiene un radio de 10 m, el área semicircular será: $$ A_{semicirculo} = \frac{1}{2} \pi (10)^2 = 50\pi , m^2 $$

Calcular el área de la fuente cuadrada

El área de un cuadrado se calcula con la fórmula ( A = l^2 ), donde ( l ) es el lado del cuadrado. La fuente tiene un lado de 10 m, entonces su área es: $$ A_{fuente} = (10)^2 = 100 , m^2 $$

Calcular el área disponible para el césped

Para encontrar el área disponible, restamos el área de la fuente del área semicircular: $$ A_{disponible} = A_{semicirculo} - A_{fuente} = 50\pi - 100 , m^2 $$

Reescribir el área disponible en una forma más útil

Para expresar el área disponible en un formato más útil, podemos factorizar: $$ A_{disponible} = 25(2\pi - 4) , m^2 $$

El área disponible para cubrir con césped es ( 25(2\pi - 4) , m^2 ).

More Information

En este problema, trabajamos con áreas de formas geométricas básicas, como círculos y cuadrados. La conexión entre la geometría y el cálculo de áreas es fundamental en problemas de este tipo.

Tips

Confundir las fórmulas para el área del círculo y del cuadrado, lo que puede llevar a resultados incorrectos en el cálculo de áreas.
Olvidar que el área del jardín es semicircular, lo que puede causar un cálculo incorrecto del área total.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!