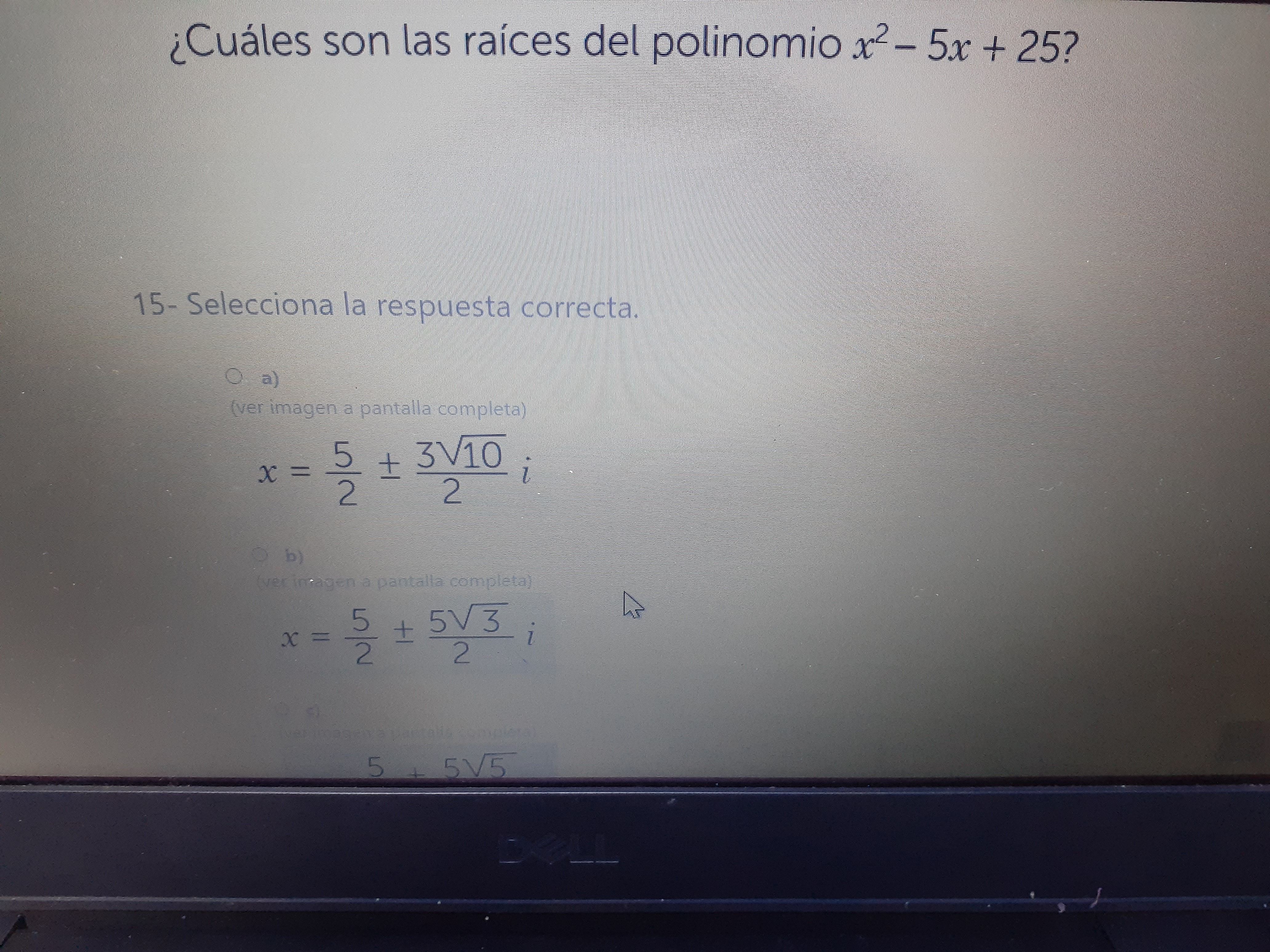
¿Cuáles son las raíces del polinomio x² - 5x + 25?
Understand the Problem
La pregunta pide encontrar las raíces del polinomio cuadrático dado: x² - 5x + 25. Esto implica utilizar la fórmula cuadrática o completar el cuadrado para hallar los valores de x que satisfacen la ecuación.
Answer
$x = \frac{5}{2} \pm \frac{5\sqrt{3}}{2}i$
Answer for screen readers
b) $x = \frac{5}{2} \pm \frac{5\sqrt{3}}{2}i$
Steps to Solve
- Identify the coefficients
The given quadratic polynomial is $x^2 - 5x + 25$. Comparing this with the general form of a quadratic equation $ax^2 + bx + c = 0$, we have $a = 1$, $b = -5$, and $c = 25$.
- Apply the quadratic formula
The quadratic formula is given by:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Plugging in the values of $a$, $b$, and $c$, we get:
$$ x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(1)(25)}}{2(1)} $$
- Simplify the expression
Simplify the expression under the square root:
$$ x = \frac{5 \pm \sqrt{25 - 100}}{2} $$
$$ x = \frac{5 \pm \sqrt{-75}}{2} $$
- Express the square root of a negative number in terms of $i$
Since $\sqrt{-1} = i$, we can rewrite $\sqrt{-75}$ as $\sqrt{75} \cdot i$. Also, $\sqrt{75} = \sqrt{25 \cdot 3} = 5\sqrt{3}$. Therefore:
$$ x = \frac{5 \pm 5\sqrt{3}i}{2} $$
- Separate into two roots
The two roots are:
$$ x = \frac{5}{2} \pm \frac{5\sqrt{3}}{2}i $$
b) $x = \frac{5}{2} \pm \frac{5\sqrt{3}}{2}i$
More Information
The roots of the quadratic equation are complex conjugates. This means the quadratic equation does not intersect the x-axis.
Tips
- Incorrectly applying the quadratic formula.
- Making errors when simplifying the square root of a negative number. For example, not extracting the $i$ from $\sqrt{-75}$.
- Incorrectly identifying the coefficients $a$, $b$, and $c$ from the given quadratic equation.
AI-generated content may contain errors. Please verify critical information