Calculate the current using KVL and KCL for the electrical circuit including the current, voltage, and resistance.
Understand the Problem
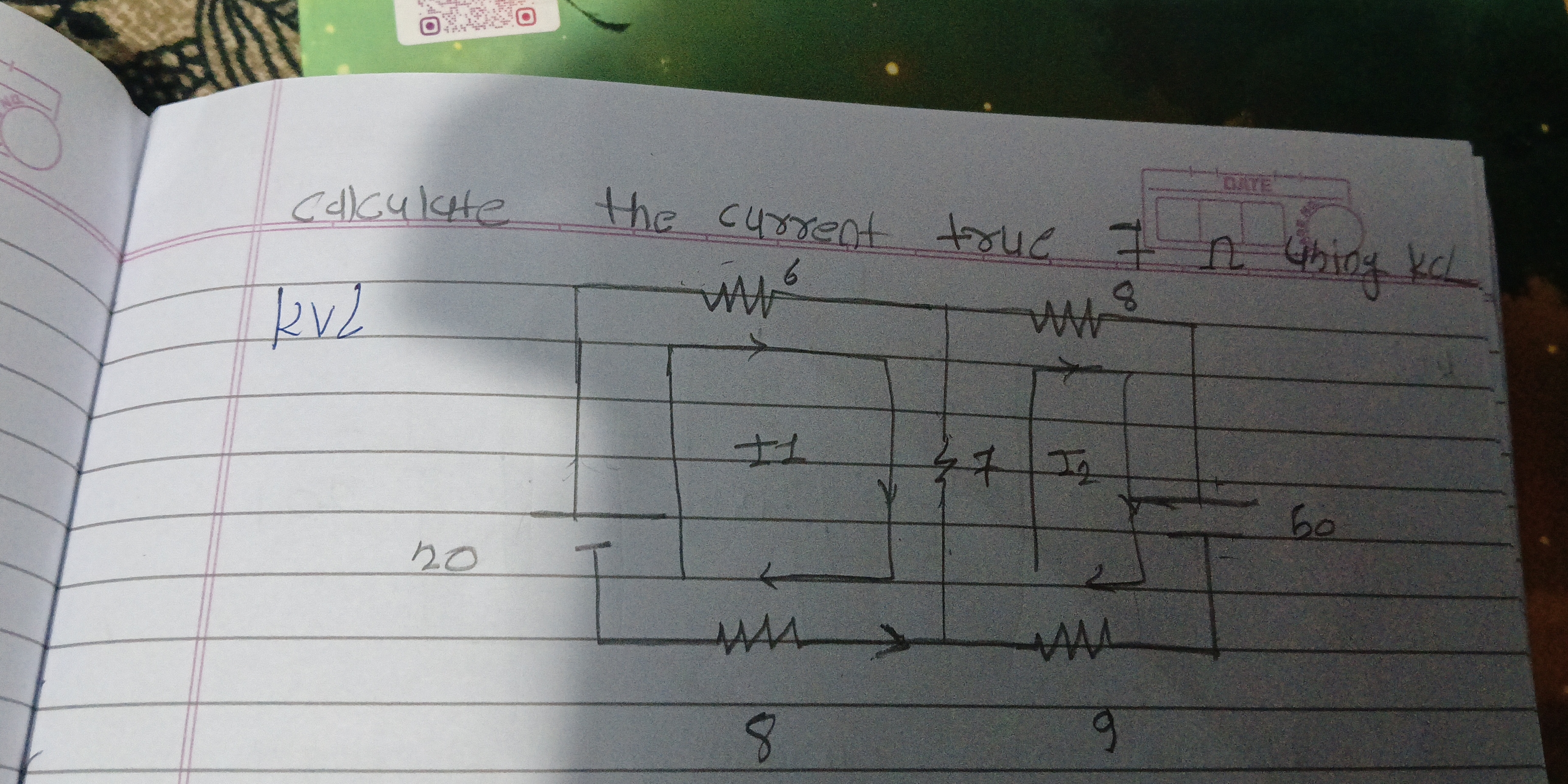
The question presents an electrical circuit and asks to calculate the true current, presumably in different parts of the circuit; the writing is illegible, but the symbols used are electrical engineering conventions. The question mentions KVL (Kirchhoff's Voltage Law) and KCL (Kirchhoff's Current Law), implying these techniques should be used to solve the circuit. We must calculate the current true using KCL.
Answer
$I_7 = -\frac{340}{87} \, \text{A}$
Answer for screen readers
$I_7 = -\frac{340}{87} \approx -3.908 , \text{A}$
Steps to Solve
- Redraw and Label the Circuit
First, redraw the circuit diagram to make it clearer and label all the components and nodes. I think the $7 \Omega$ resistor is actually $8 \Omega$. We know that is the case because there is another $7 \Omega$ label which is the current we need to find. The circuit contains:
- A 20V voltage source
- A 60V voltage source
- Three resistors: $6 \Omega$, $8 \Omega$, and $9 \Omega$
- The goal is to find the current $I_2$ flowing through what looks like an $8 \Omega$ resistor but it represents a current that you will find. Since the initial writing is not clear let's rename it to $I_7$
- Two other currents are labeled $I_1$ and $I_2$; however, it appears that $I_2$ is actually $I_7$.
- Apply KCL at Node A
Apply Kirchhoff's Current Law (KCL) at Node A. KCL states that the sum of currents entering a node must equal the sum of currents leaving the node. $$ I_1 = I_7 + I_2$$
- Apply KVL in Loop 1
Apply Kirchhoff's Voltage Law (KVL) to the loop containing the 20V source, the $6\Omega$ resistor, and the $8\Omega$ resistor. $$ 20 - 6I_1 - 8I_2 = 0$$
- Apply KVL in Loop 2
Apply Kirchhoff's Voltage Law (KVL) to the loop containing the $8\Omega$ resistor, the $9\Omega$ resistor, and the 60V source $$ -8I_2 + 9I_7 + 60 = 0$$
- Express $I_1$ in terms of $I_2$ from Loop 1 KVL
From the KVL equation for Loop 1, express (I_1) in terms of (I_2): $$6I_1 = 20 - 8I_2$$ $$I_1 = \frac{20 - 8I_2}{6} = \frac{10 - 4I_2}{3}$$
- Express $I_7$ in terms of $I_2$ from Loop 2 KVL
From the KVL equation for Loop 2, express (I_7) in terms of (I_2): $$9I_7 = 8I_2 - 60$$ $$I_7 = \frac{8I_2 - 60}{9}$$
- Substitute $I_1$ and $I_7$ into the KCL equation
Substitute the expressions for $I_1$ and $I_7$ into the KCL equation from Node A: $$ \frac{10 - 4I_2}{3} = \frac{8I_2 - 60}{9} + I_2 $$
- Solve for $I_2$
Multiply through by 9 to eliminate fractions: $$ 3(10 - 4I_2) = (8I_2 - 60) + 9I_2 $$ $$ 30 - 12I_2 = 8I_2 - 60 + 9I_2 $$ $$ 30 - 12I_2 = 17I_2 - 60 $$ $$ 90 = 29I_2 $$ $$ I_2 = \frac{90}{29} $$
- Solve for $I_7$
Using the solution for $I_2$, we can now calculate the final answer $I_7$ $$I_7 = (\frac{8I_2 - 60}{9})$$ $$I_7 = (\frac{8(\frac{90}{29}) - 60}{9})$$ $$I_7 = (\frac{\frac{720}{29} - \frac{1740}{29}}{9})$$ $$I_7 = (\frac{\frac{-1020}{29}}{9})$$ $$I_7 = \frac{-1020}{29*9} = \frac{-1020}{261} = \frac{-340}{87} \approx -3.908 A$$
$I_7 = -\frac{340}{87} \approx -3.908 , \text{A}$
More Information
The current flowing through the $7 \Omega$ (that is, $I_7$), calculated using KCL and KVL, is approximately -3.908 amps. The negative sign indicates that the actual current direction is opposite to the direction initially assumed in the circuit diagram.
Tips
- Incorrectly applying KVL/KCL: Failing to correctly sum voltages around a loop (KVL) or currents at a node (KCL) can lead to incorrect equations. Always double-check the signs and directions of voltages and currents.
- Algebraic Errors: Mistakes in algebraic manipulation when solving the system of equations are very common. Take your time, and double-check each step.
- Forgetting Units: Always include units (e.g., Amps for current) in your final answer.
- Misinterpreting the Circuit Diagram: It is imperative to accurately interpret the circuit diagram including the components and their connections.
To avoid these mistakes:
- Practice applying KVL and KCL to various circuits.
- Double-check each step in your algebraic manipulations.
- Always include units in your final answer.
- Pay close attention to the circuit diagram.
AI-generated content may contain errors. Please verify critical information