Convert the following: (a) (1001)8 = ( )2 (b) (.45)10 = ( )8 (c) (2CC)16 = ( )5. Explain non-inverting amplifier. Define canonical form of Boolean expressions.
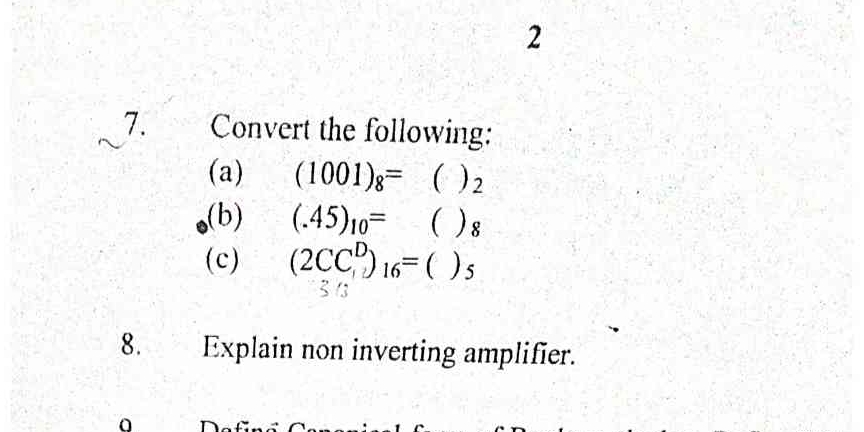
Understand the Problem
The question asks to convert numbers from different bases (octal, decimal, and hexadecimal) to specified bases (binary, octal, and decimal). Additionally, it requests an explanation of a non-inverting amplifier and the definition of canonical form in Boolean algebra.
Answer
(a) \( (1001)₈ = (10010001)₂ \) (b) \( (.45)_{10} \approx (0.34631)₈ \) (c) \( (2CC)_{16} = (10331)_{5} \)
Answer for screen readers
(a) ( (1001)₈ = (10010001)₂ )
(b) ( (.45)_{10} \approx (0.34631)₈ )
(c) ( (2CC){16} = (10331){5} )
Steps to Solve
- Convert (1001)₈ to Binary (Base 2)
Each octal digit corresponds to a 3-bit binary number:
- (1 = 001)
- (0 = 000)
- (0 = 000)
- (1 = 001)
So, combining them gives:
[
(1001)₈ = 001000000001 = (10010001)₂
]
- Convert (.45)₁₀ to Octal (Base 8)
To convert a decimal fraction to octal:
- Multiply by 8:
(0.45 \times 8 = 3.6) → Take (3) as the first digit. - Take the decimal part (0.6) and multiply again by 8:
(0.6 \times 8 = 4.8) → Take (4) as the next digit. - Continue with (0.8):
(0.8 \times 8 = 6.4) → Take (6). - Continue with (0.4):
(0.4 \times 8 = 3.2) → Take (3). - Continue with (0.2):
(0.2 \times 8 = 1.6) → Take (1). - Continue with (0.6) for further digits if needed.
So we have:
[
(.45)_{10} \approx (0.34631)₈
]
- Convert (2CC)₁₆ to Base 5
First, convert hexadecimal to decimal:
[
(2CC)_{16} = 2 \times 16^2 + 12 \times 16^1 + 12 \times 16^0 = 2 \times 256 + 12 \times 16 + 12 \times 1 = 512 + 192 + 12 = 716
]
Next, convert decimal to base 5:
- Divide by 5, keeping track of the remainders:
(716 \div 5 = 143) remainder (1)
(143 \div 5 = 28) remainder (3)
(28 \div 5 = 5) remainder (3)
(5 \div 5 = 1) remainder (0)
(1 \div 5 = 0) remainder (1)
Reading remainders from bottom to top gives:
[
(716){10} = (10331){5}
]
(a) ( (1001)₈ = (10010001)₂ )
(b) ( (.45)_{10} \approx (0.34631)₈ )
(c) ( (2CC){16} = (10331){5} )
More Information
- Octal to binary conversion breaks down each octal digit into 3 bits.
- Decimal fractions convert by repeated multiplication and taking the integer part.
- Hexadecimal to decimal uses powers of 16, while decimal to another base involves successive division by that base and collecting remainders.
Tips
- Miscounting bits when converting from octal to binary.
- Forgetting to continue multiplying decimal fractions until reaching sufficient precision or until repetition is observed in the decimal part.
- Making arithmetic mistakes in the conversion from hexadecimal to decimal.
AI-generated content may contain errors. Please verify critical information