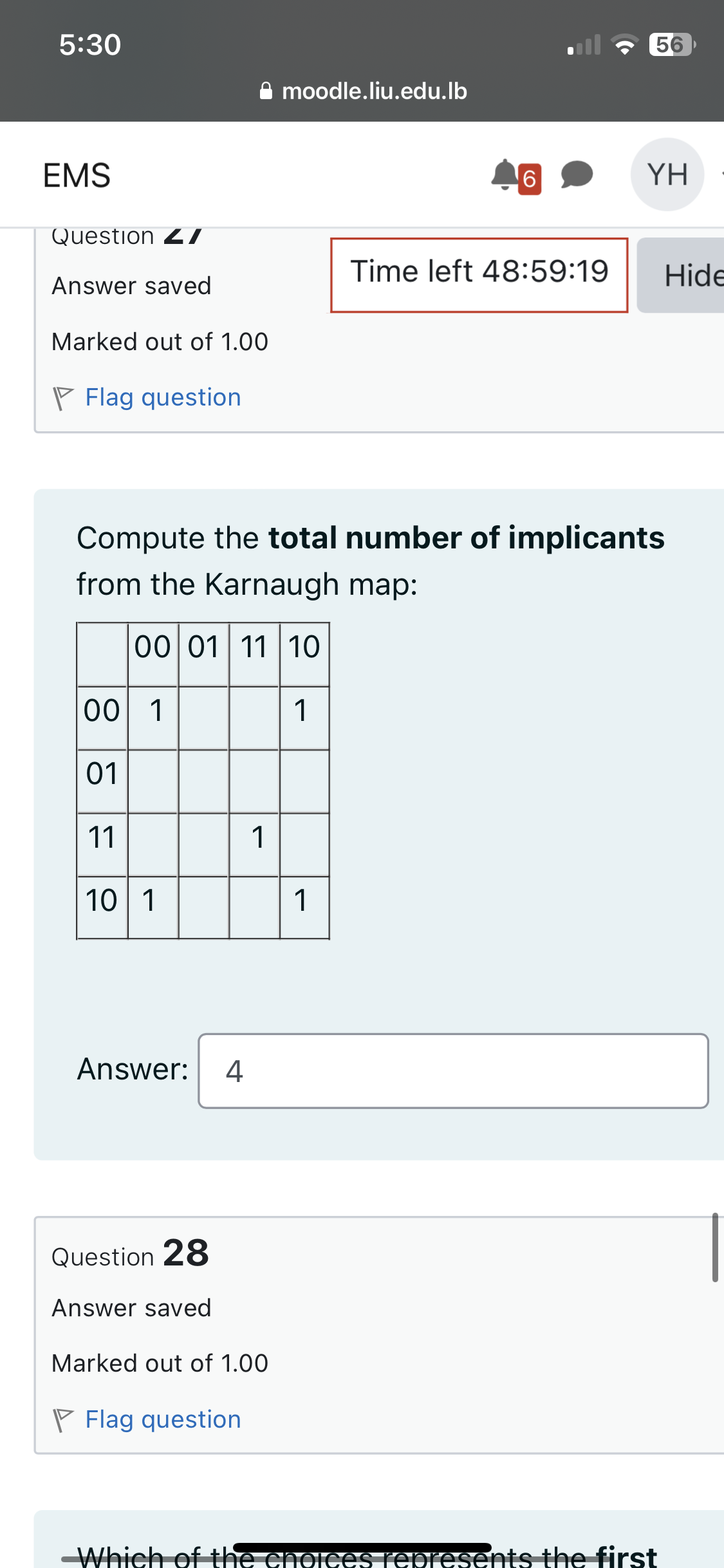
Compute the total number of implicants from the Karnaugh map.

Understand the Problem

The question is asking for the total number of implicants that can be derived from the provided Karnaugh map, which is a method used in Boolean algebra for simplifying expressions.

Answer

4

Steps to Solve

Identify Non-Zero Cells in the Karnaugh Map

Examine the given Karnaugh map and identify all the cells that contain '1'. These represent the minterms. In our case, the map has '1's in the following cells:

(00, 00) -> (0,0)
(00, 01) -> (0,1)
(01, 10) -> (1,2)
(11, 10) -> (2,2)
(10, 01) -> (1,0)
(10, 11) -> (2,0)
(11, 11) -> (2,1)

Group the '1's into Implicants

Next, we need to group the identified '1's in sizes of 1, 2, 4, or 8, while ensuring we respect the rules of the Karnaugh map:

Individual '1's count as single implicants.
Pairs or groups of adjacent '1's can form larger implicants.

Mapping the positions, we can create the following groups:

Group 1: (00, 00), (00, 01)
Group 2: (01, 10), (11, 10), (10, 01), (10, 11)

Count the Unique Implicants

After determining the overlapping groups, count how many unique implicants you have. In this problem:

Group 1 (2 cells) forms an implicant.
Group 2 (4 cells) forms another implicant.

Thus, the total number of implicants is 4.

The total number of implicants from the Karnaugh map is 4.

More Information

In a Karnaugh map, implicants are crucial as they represent the simplest forms of the logical expression. This exercise underscores the importance of identifying and grouping '1's effectively for simplification.

Tips

Ignoring Adjacent Groups: Ensure you recognize grouped ones properly as they can share borders and form larger implicants.
Miscounting the Grouping: Sometimes groups can overlap, leading to double counting. Always focus on unique implicants.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!