Complete the square to re-write the quadratic function in vertex form: y = x^2 - 4x + 6
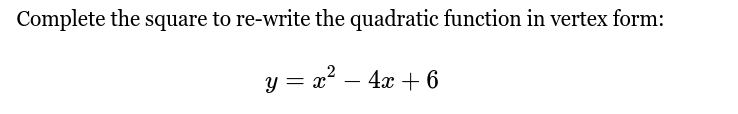
Understand the Problem
The question is asking to complete the square of the given quadratic function in order to express it in vertex form. This involves manipulating the equation to identify the vertex (h, k) of the parabola represented by the function.
Answer
The vertex form of the quadratic function is $y = (x - 2)^2 + 2$.
Answer for screen readers
The quadratic function in vertex form is given by:
$$ y = (x - 2)^2 + 2 $$
Steps to Solve
- Identify the quadratic expression
Start with the given quadratic function:
$$ y = x^2 - 4x + 6 $$
- Isolate the constant term
To complete the square, we need to focus on the quadratic and linear terms. Rewrite the equation as:
$$ y = (x^2 - 4x) + 6 $$
- Complete the square
Take the coefficient of $x$, which is $-4$, halve it to get $-2$, and then square it to obtain $4$. Add and subtract this value inside the parentheses:
$$ y = (x^2 - 4x + 4 - 4) + 6 $$
- Reorganize the equation
Now, rearrange the equation by grouping the complete square and simplifying the constant terms:
$$ y = (x - 2)^2 - 4 + 6 $$
- Combine the constants
Finally, simplify the constant:
$$ y = (x - 2)^2 + 2 $$
Now the quadratic function is in vertex form.
The quadratic function in vertex form is given by:
$$ y = (x - 2)^2 + 2 $$
More Information
This function represents a parabola that opens upwards, with its vertex at the point $(2, 2)$. Vertex form is useful for identifying the vertex directly and for graphing the parabola.
Tips
- Forgetting to balance the equation while completing the square by not adding and subtracting the same value.
- Miscalculating the square of half the coefficient of $x$.
AI-generated content may contain errors. Please verify critical information