Can you explain the domain and range of basic mathematical functions provided in the image?
Understand the Problem
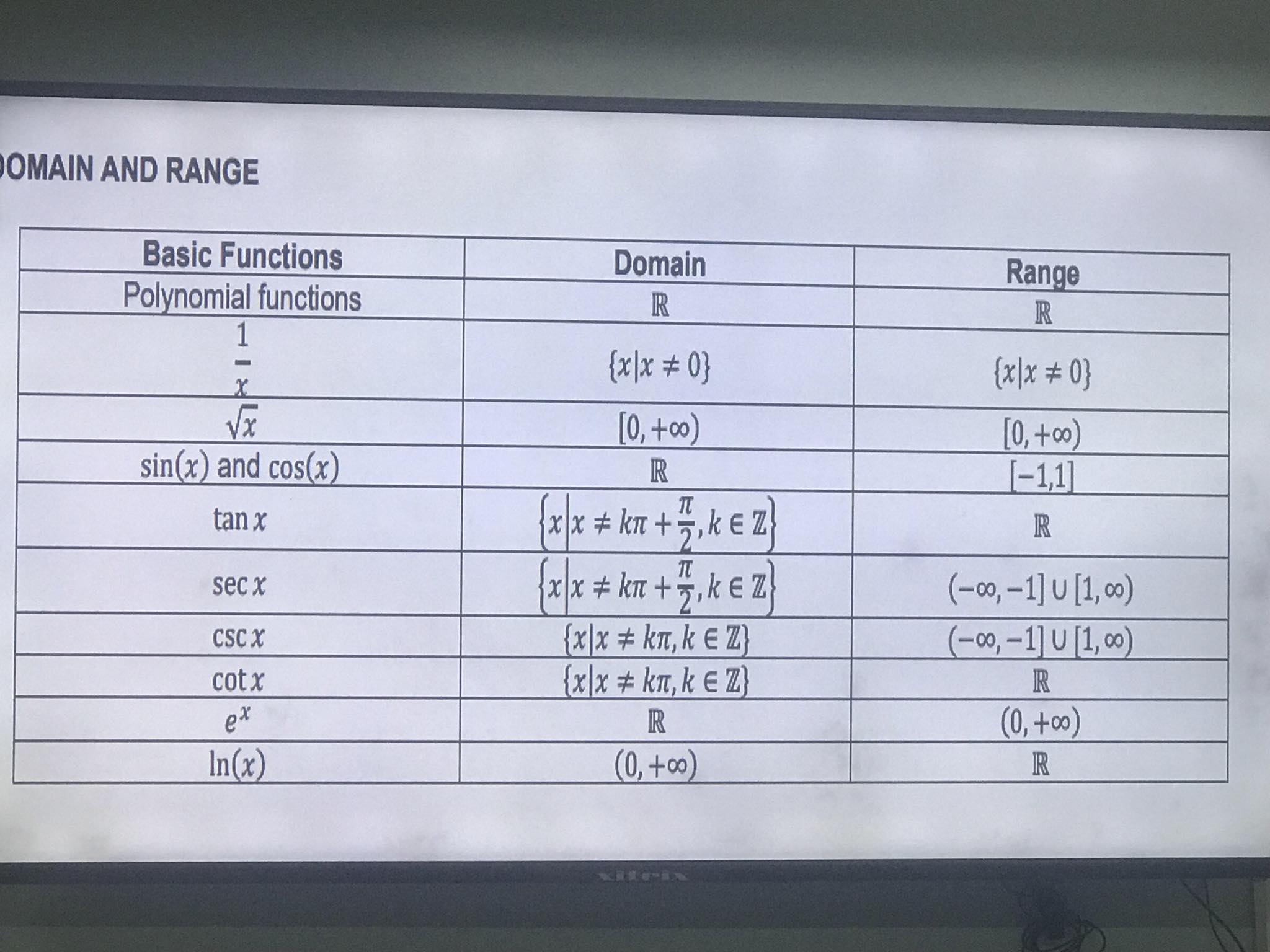
The question presents a table showing the basic functions along with their domains and ranges. It seeks to summarize how each function behaves within the context of mathematics, particularly focusing on their permissible input values (domain) and the output values they can produce (range).
Answer
1. $\frac{1}{x}$: Domain: $\{x | x \neq 0\}$, Range: $\{y | y \neq 0\}$ 2. $\sqrt{x}$: Domain: $[0, +\infty)$, Range: $[0, +\infty)$ 3. $\sin(x)$ and $\cos(x)$: Domain: $\mathbb{R}$, Range: $[-1, 1]$ 4. $\tan(x)$: Domain: $\{x | x \neq k\frac{\pi}{2}, k \in \mathbb{Z}\}$, Range: $\mathbb{R}$ 5. $\sec(x)$: Domain: $\{x | x \neq k\frac{\pi}{2}, k \in \mathbb{Z}\}$, Range: $(-\infty, -1] \cup [1, +\infty)$ 6. $\csc(x)$: Domain: $\{x | x \neq k\pi, k \in \mathbb{Z}\}$, Range: $(-\infty, -1] \cup [1, +\infty)$ 7. $\cot(x)$: Domain: $\{x | x \neq k\pi, k \in \mathbb{Z}\}$, Range: $\mathbb{R}$ 8. $e^x$: Domain: $\mathbb{R}$, Range: $(0, +\infty)$ 9. $\ln(x)$: Domain: $(0, +\infty)$, Range: $\mathbb{R}$
Answer for screen readers
The domain and range for the functions presented are summarized as follows:
-
$\frac{1}{x}$:
- Domain: ${x | x \neq 0}$
- Range: ${y | y \neq 0}$
-
$\sqrt{x}$:
- Domain: $[0, +\infty)$
- Range: $[0, +\infty)$
-
$\sin(x)$ and $\cos(x)$:
- Domain: $\mathbb{R}$
- Range: $[-1, 1]$
-
$\tan(x)$:
- Domain: ${x | x \neq k\frac{\pi}{2}, k \in \mathbb{Z}}$
- Range: $\mathbb{R}$
-
$\sec(x)$:
- Domain: ${x | x \neq k\frac{\pi}{2}, k \in \mathbb{Z}}$
- Range: $(-\infty, -1] \cup [1, +\infty)$
-
$\csc(x)$:
- Domain: ${x | x \neq k\pi, k \in \mathbb{Z}}$
- Range: $(-\infty, -1] \cup [1, +\infty)$
-
$\cot(x)$:
- Domain: ${x | x \neq k\pi, k \in \mathbb{Z}}$
- Range: $\mathbb{R}$
-
$e^x$:
- Domain: $\mathbb{R}$
- Range: $(0, +\infty)$
-
$\ln(x)$:
- Domain: $(0, +\infty)$
- Range: $\mathbb{R}$
Steps to Solve
-
Understanding Domain and Range The domain of a function is the set of all possible input values (x-values) for which the function is defined, while the range is the set of all possible output values (y-values) the function can produce.
-
Analyzing Each Function's Domain
- The polynomial function $\frac{1}{x}$ is undefined when $x = 0$, so its domain is ${x | x \neq 0}$.
- The square root function $\sqrt{x}$ is only defined for non-negative inputs, giving it a domain of $[0, +\infty)$.
- The sine and cosine functions $\sin(x)$ and $\cos(x)$ are defined for all real numbers, thus their domain is $\mathbb{R}$.
- Analyzing Each Function's Range
- For the function $\frac{1}{x}$, as $x$ approaches zero, the output can become arbitrarily large or small (positive or negative), hence the range is ${y | y \neq 0}$.
- The output of the square root function $\sqrt{x}$ is always non-negative, resulting in a range of $[0, +\infty)$.
- $\sin(x)$ and $\cos(x)$ oscillate between -1 and 1, thus their range is $[-1, 1]$.
- Summary of Properties
- For the tangent function $\tan(x)$, the domain excludes points where $\cos(x) = 0$ (i.e., $x \neq k\frac{\pi}{2}$), and it spans all real numbers, resulting in a range of $\mathbb{R}$.
- The secant function $\sec(x)$ is also undefined where $\cos(x) = 0$, but its range consists of two intervals $(-\infty, -1] \cup [1, +\infty)$.
- For $\tan^{-1}(x)$ and other expressions involving inverse trigonometric functions, similar reasoning applies, leading to specific domains and ranges based on where the function remains well-defined.
- Other Functions
- The exponential function $e^x$ has a domain of all real numbers ($\mathbb{R}$) and produces positive outputs, leading to a range of $(0, +\infty)$.
- The natural logarithm function $\ln(x)$, defined for positive x, has a domain of $(0, +\infty)$ and a range of $\mathbb{R}$.
The domain and range for the functions presented are summarized as follows:
-
$\frac{1}{x}$:
- Domain: ${x | x \neq 0}$
- Range: ${y | y \neq 0}$
-
$\sqrt{x}$:
- Domain: $[0, +\infty)$
- Range: $[0, +\infty)$
-
$\sin(x)$ and $\cos(x)$:
- Domain: $\mathbb{R}$
- Range: $[-1, 1]$
-
$\tan(x)$:
- Domain: ${x | x \neq k\frac{\pi}{2}, k \in \mathbb{Z}}$
- Range: $\mathbb{R}$
-
$\sec(x)$:
- Domain: ${x | x \neq k\frac{\pi}{2}, k \in \mathbb{Z}}$
- Range: $(-\infty, -1] \cup [1, +\infty)$
-
$\csc(x)$:
- Domain: ${x | x \neq k\pi, k \in \mathbb{Z}}$
- Range: $(-\infty, -1] \cup [1, +\infty)$
-
$\cot(x)$:
- Domain: ${x | x \neq k\pi, k \in \mathbb{Z}}$
- Range: $\mathbb{R}$
-
$e^x$:
- Domain: $\mathbb{R}$
- Range: $(0, +\infty)$
-
$\ln(x)$:
- Domain: $(0, +\infty)$
- Range: $\mathbb{R}$
More Information
Understanding the domain and range is crucial for knowing how functions behave. Each function has specific restrictions that dictate where they can be applied and what outputs can be expected. This is fundamental in fields like calculus and mathematical modeling.
Tips
- Forgetting to exclude values from the domain can lead to incorrect interpretations of the function's behavior. Always double-check which values might cause undefined behaviors (like division by zero).
- Confusing domain and range; remember that domain refers to possible inputs and range to possible outputs.
AI-generated content may contain errors. Please verify critical information