Calculate the value of $N_t$ given the formula $N_t = 300(1 - 0.12)^7$
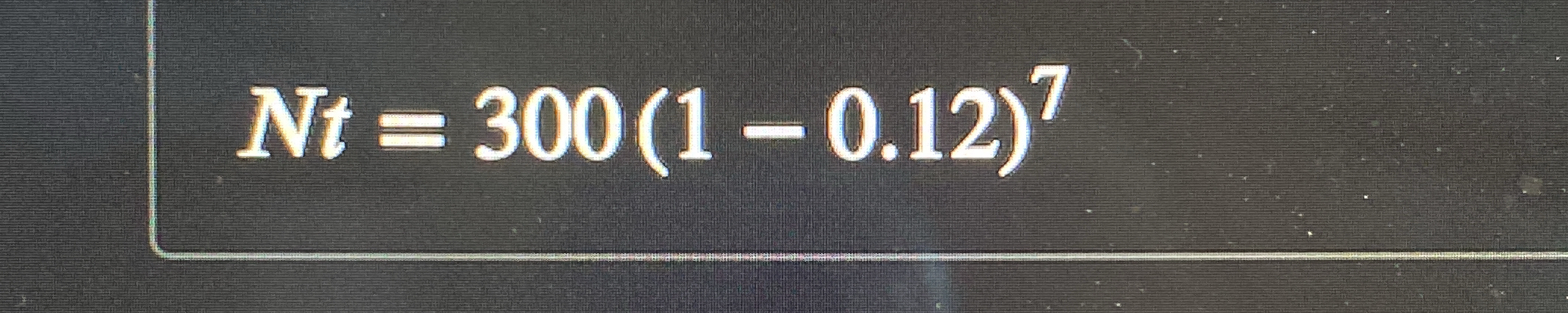
Understand the Problem
The problem requires to calculating the value of $N_t$ given the formula $N_t = 300(1 - 0.12)^7$. This is a straightforward mathematical calculation involving exponentiation and subtraction.
Answer
$N_t \approx 123.09$
Answer for screen readers
$N_t \approx 123.09$
Steps to Solve
- Calculate the value inside the parentheses
First subtract 0.12 from 1:
$1 - 0.12 = 0.88$
- Raise the result to the power of 7
Calculate $0.88^7$:
$0.88^7 \approx 0.4103$
- Multiply by 300
Multiply the result from the previous step by 300 to find $N_t$:
$N_t = 300 \times 0.4103 \approx 123.09$
$N_t \approx 123.09$
More Information
The value of $N_t$ is approximately 123.09. This type of calculation is often used in modeling population dynamics or depreciation.
Tips
A common mistake is performing the multiplication before exponentiation, which violates the order of operations (PEMDAS/BODMAS). Another mistake is rounding intermediate values too early, which can affect the accuracy of the final answer.
AI-generated content may contain errors. Please verify critical information