Calculate the integral ∫ from -1 to 1 of x e^(x^2) dx.
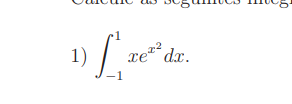
Understand the Problem
The question is asking to calculate the integral of the function x * e^(x^2) over the interval from -1 to 1. This involves finding the definite integral, which may require techniques such as integration by parts or substitution.
Answer
The integral evaluates to $0$.
Answer for screen readers
The value of the integral is $0$.
Steps to Solve
- Recognizing the integral's properties
The integral $\int_{-1}^{1} x e^{x^2} , dx$ is an odd function because $f(-x) = -f(x)$. This means that the integral over a symmetric interval around zero (from $-1$ to $1$) will equal zero.
- Confirming that f(x) is odd
To confirm that $f(x) = x e^{x^2}$ is odd:
- Compute $f(-x)$: $$ f(-x) = -x e^{(-x)^2} = -x e^{x^2} = -f(x) $$ This shows that our function is indeed odd.
- Evaluating the definite integral
Since $f(x)$ is an odd function: $$ \int_{-1}^{1} x e^{x^2} , dx = 0 $$ This result confirms that the integral of an odd function over a symmetric interval is zero.
The value of the integral is $0$.
More Information
The integral of an odd function over a symmetric interval always results in zero. This property is very useful in calculus, as it simplifies many calculations.
Tips
- Failing to recognize that the function is odd and incorrectly calculating the integral.
- Mixing up the limits of integration or the properties of even and odd functions.
AI-generated content may contain errors. Please verify critical information